
【题目】庄子说:“一尺之锤,日取其半,万世不竭”,这句话描述的是一个数列问题,现用程序框图描述,如图所示,若输入某个正整数n后,输出的S∈( ![]() ,
, ![]() ),则输入的n的值为( )
),则输入的n的值为( )
A.7
B.6
C.5
D.4
【答案】C
【解析】解:框图首先给累加变量S赋值0,给循环变量k赋值1,
输入n的值后,执行循环体,S= ![]() ,k=1+1=2;
,k=1+1=2;
判断2>n不成立,执行循环体,S= ![]() ,k=2+1=3;
,k=2+1=3;
判断3>n不成立,执行循环体,S= ![]() ,k=3+1=4;
,k=3+1=4;
判断4>n不成立,执行循环体,S= ![]() ,k=4+1=5.
,k=4+1=5.
判断5>n不成立,执行循环体,S= ![]() ,k=4+1=6.
,k=4+1=6.
判断6>n不成立,执行循环体,S= ![]() ,k=4+1=7.
,k=4+1=7.
…
由于输出的S∈( ![]() ,
, ![]() ),可得:当S=
),可得:当S= ![]() ,k=6时,应该满足条件6>n,即:5≤n<6,
,k=6时,应该满足条件6>n,即:5≤n<6,
可得输入的正整数n的值为5.
故选:C.
【考点精析】掌握程序框图是解答本题的根本,需要知道程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
(Ⅰ)若a=1,解不等式f(x)<6;
(Ⅱ)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+y2+2y﹣7=0和点N(0,1),动圆P经过点N且与圆M相切,圆心P的轨迹为曲线E.
(1)求曲线E的方程;
(2)点A是曲线E与x轴正半轴的交点,点B、C在曲线E上,若直线AB、AC的斜率k1 , k2 , 满足k1k2=4,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
第一组 | [105,110] | 15 | 0.3 |
第二组 | [110,115) | 30 | 0.3 |
第三组 | [115,120) | x | 0.4 |
第四组 | [120,125) | 100 | 0.5 |
第五组 | [125,130) | 120 | 0.6 |
第六组 | [130,135) | 195 | y |
(Ⅰ)补全所给的频率分布直方图,并求n,x,y的值;
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取9份进行展出,并从9份试卷中选出两份作为优秀试卷,优秀试卷在[115,120)中的分数记为ξ,求随机变量ξ的分布列及期望.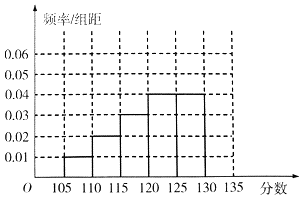
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P(2,0),且正方形ABCD内接于⊙O:x2+y2=1,M、N分别为边AB、BC的中点.当正方形ABCD绕圆心O旋转时, ![]() 的取值范围为 .
的取值范围为 . 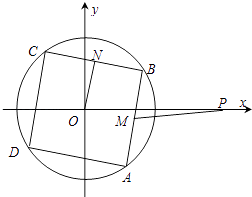
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣ax﹣3(a∈R).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2(f'(x)+ ![]() )在区间(t,3)上总不是单调函数,求m的取值范围;
)在区间(t,3)上总不是单调函数,求m的取值范围;
(Ⅲ)求证: ![]() ×
× ![]() ×
× ![]() ×…×
×…× ![]() <
< ![]() (n≥2,n∈N*).
(n≥2,n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月某校高三年级1600名学生参加了教育局组织的期末统考,已知数学考试成绩X~N(100,σ2)(试卷满分为150分).统计结果显示数学考试成绩在80分到120分之间的人数约为总人数的 ![]() ,则此次统考中成绩不低于120分的学生人数约为( )
,则此次统考中成绩不低于120分的学生人数约为( )
A.80
B.100
C.120
D.200
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com