
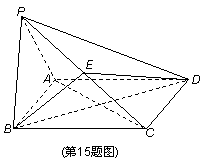
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,
BP=BC,E为PC的中点.
(1)求证:AP∥平面BDE;
(2)求证:BE⊥平面PAC.
 |
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有 .
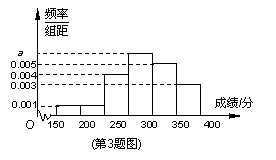 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的各项都为正数,且对任意n∈N*,a2n-1,a2n,a2n+1成等差数列,
a2n,a2n+1,a2n+2成等比数列.
(1)若a2=1,a5=3,求a1的值;
(2)设a1<a2,求证:对任意n∈N*,且n≥2,都有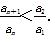 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆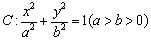 的左、右焦点分别为
的左、右焦点分别为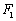 、
、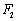 ,过
,过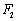 作直线
作直线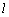 与椭圆
与椭圆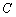 交于点
交于点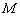 、
、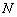 .
.
(1)若椭圆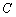 的离心率为
的离心率为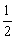 ,右准线的方程为
,右准线的方程为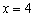 ,
,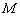 为椭圆
为椭圆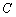 上顶点,直线
上顶点,直线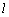 交右准线于点
交右准线于点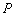 ,求
,求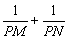 的
的 值;
值;
(2)当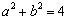 时,设
时,设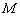 为椭圆
为椭圆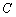 上第一象限内的点,直线
上第一象限内的点,直线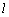 交
交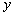 轴于点
轴于点 ,
,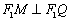 ,证明:点
,证明:点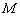 在定直线上.
在定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com