
设函数
 .
.
(1)当 时,求函数
时,求函数 的极大值;
的极大值;
(2)若函数 的图象与函数
的图象与函数 的图象有三个不同的交点,求
的图象有三个不同的交点,求 的取值范围;
的取值范围;
(3)设 ,当
,当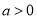 时,求函数
时,求函数 的单调减区间.
的单调减区间.
(1)5;(2) ;(3)①当
;(3)①当 时,函数
时,函数 的单调减区间为
的单调减区间为 ;
;
②当 时,函数
时,函数 的单调减区间为
的单调减区间为 ,
, ;
;
③当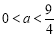 时,函数
时,函数 的单调减区间为
的单调减区间为 ,
, ,
,  .
.
【解析】
试题分析:(1)当 时,函数
时,函数 是一个具体的三次函数,只须求出
是一个具体的三次函数,只须求出 的导函数,并令它为零求得其根;然后列出
的导函数,并令它为零求得其根;然后列出 的取值范围与
的取值范围与 的符号及
的符号及 单调性的变化情况表,由此表可求得函数
单调性的变化情况表,由此表可求得函数 的极大值;(2)函数
的极大值;(2)函数 的图象与函数
的图象与函数 的图象有三个不同的交点,等价于方程
的图象有三个不同的交点,等价于方程 即
即 有三个不同的实数根,也等价于方程
有三个不同的实数根,也等价于方程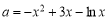 有三个不同的实数根,从而可转化为直线
有三个不同的实数根,从而可转化为直线 与函数
与函数 有三个不同的交点,画草图可知必须且只需:
有三个不同的交点,画草图可知必须且只需: ,所以利用导数求出函数
,所以利用导数求出函数 的极小值和极大值即可;(3)注意到函数
的极小值和极大值即可;(3)注意到函数 的图象与函数
的图象与函数 的图象之间的关系:将函数
的图象之间的关系:将函数 在x轴上方的图象不变,而将x轴下方的图象沿x轴翻折到x轴上方即得函数
在x轴上方的图象不变,而将x轴下方的图象沿x轴翻折到x轴上方即得函数 的图象,由此可知要求函数
的图象,由此可知要求函数 的单调减区间,只须先求出函数
的单调减区间,只须先求出函数 的单调区间,并求出
的单调区间,并求出 的所有零点,结合图象就可写出函数
的所有零点,结合图象就可写出函数 的单调减区间;注意分类讨论.
的单调减区间;注意分类讨论.
试题解析:(1)当 时,由
时,由 =0,得
=0,得 或
或 , 2分
, 2分
列表如下:
|
| -1 |
| 3 |
|
| + | 0 | - | 0 | + |
| 递增 | 极大 | 递减 | 极小 | 递增 |
所以当 时,函数
时,函数 取得极大值为5. 4分
取得极大值为5. 4分
(2)由 ,得
,得 ,即
,即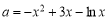 , 6分
, 6分
令 ,则
,则 ,
,
列表,得
|
|
|
| 1 |
|
| - | 0 | + | 0 | - |
| 递减 | 极小值 | 递增 | 极大值2 | 递减 |
8分
由题意知,方程 有三个不同的根,故
有三个不同的根,故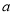 的取值范围是
的取值范围是 . 10分
. 10分
(3)因为 ,
,
所以当 时,
时, 在R上单调递增;
在R上单调递增;
当 时,
时, 的两根为
的两根为 ,且
,且 ,
,
所以此时 在
在 上递增,在
上递增,在 上递减,在
上递减,在 上递增; 12分
上递增; 12分
令 ,得
,得 ,或
,或 (*),
(*),
当 时,方程(*)无实根或有相等实根;当
时,方程(*)无实根或有相等实根;当 时,方程(*)有两根
时,方程(*)有两根 , 13分
, 13分
从而
①当 时,函数
时,函数 的单调减区间为
的单调减区间为 ; 14分
; 14分
②当 时,函数
时,函数 的单调减区间为
的单调减区间为 ,
, ; 15分
; 15分
③当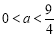 时,函数
时,函数 的单调减区间为
的单调减区间为 ,
, ,
,  . 16分
. 16分
考点:1.函数的极值;2.函数图象、方程的根及函数的零点;3.函数的单调性.


科目:高中数学 来源:2015届四川省成都市毕业班摸底测试文科数学试卷(解析版) 题型:选择题
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,一般情况下PM2.5的浓度越大,大气环境质量越差.右边的茎叶图表示的是成都市区甲乙两个监测站某10日内每天的PM2.5浓度读数(单位: ),则下列说法正确的是( )
),则下列说法正确的是( )
A、这10日内甲、乙监测站读数的极差相等
B、这10日内甲、乙监测站读数的中位数中,乙的较大
C、这10日内乙监测站读数的众数与中位数相等
D、这10日内甲、乙监测站读数的平均数相等

查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三九月月考文科数学试卷(解析版) 题型:选择题
已知数列{an}中,a1=1,an+1=an+n,若利用如右图所示的种序框图计算该数列的第10项,则判断框内的条件是( )
A.n≤8? B.n≤9? C.n≤10? D.n≤11?

查看答案和解析>>
科目:高中数学 来源:2015届四川成都树德中学高二3月月考理科数学试卷(解析版) 题型:解答题
已知以点 为圆心的圆与直线
为圆心的圆与直线 相切,过点
相切,过点 的动直线与圆
的动直线与圆 相交于
相交于 两点.
两点.
(1)求圆 的方程;
的方程;
(2)当 时,求直线
时,求直线 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市新高三起点调研考试理科数学试卷(解析版) 题型:解答题
每年5月17日为国际电信日,某市电信公司每年在电信日当天对办理应用套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.根据以往的统计结果绘出电信日当天参与活动的统计图,现将频率视为概率.
(1) 求某两人选择同一套餐的概率;
(2) 若用随机变量 表示某两人所获优惠金额的总和,求
表示某两人所获优惠金额的总和,求 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com