
已知函数 ,
,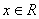 .
.
(1)若函数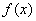 的图象在
的图象在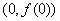 处的切线与直线
处的切线与直线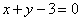 垂直,求实数
垂直,求实数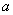 的值;
的值;
(2)求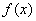 的单调区间;
的单调区间;
(3)当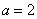 时,若对于任意
时,若对于任意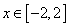 ,
,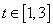 ,
,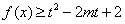 恒成立,求实数
恒成立,求实数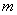 的取值范围.
的取值范围.
解:(1)∵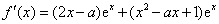
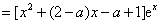
∴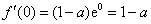 , …………………2分
, …………………2分
∵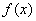 的图象在
的图象在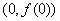 处的切线与直线
处的切线与直线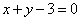 垂直,
垂直,
∴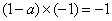 ,可得
,可得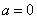 . …………………4分
. …………………4分
(2)由(1)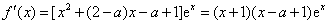 ,
,
令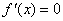 ,可得
,可得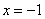 ,或
,或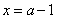 ,
,
所以当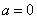 时,
时,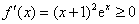 在R上恒成立,函数
在R上恒成立,函数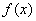 在R上单调递增; …………………6分
在R上单调递增; …………………6分
当 时,
时,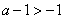 ,在
,在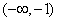 上
上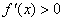 ,
,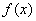 单调递增,
单调递增,
在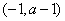 上
上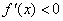 ,
,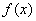 单调递减,在
单调递减,在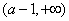 上
上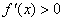 ,
,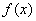 单调递增;
单调递增;
当 时,
时,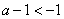 ,在
,在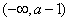 上
上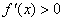 ,
,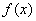 单调递增,
单调递增,
在 上
上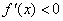 ,
,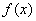 单调递减,在
单调递减,在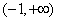 上
上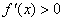 ,
,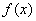 单调递增;………………8分
单调递增;………………8分
(3)当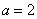 时,
时,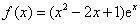 ,由(2)可知,
,由(2)可知,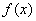 在
在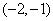 上单调递增,在
上单调递增,在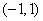 上单调递减,在
上单调递减,在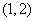 上单调递增;所以
上单调递增;所以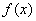 在
在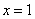 处取得极小值
处取得极小值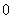 ,而
,而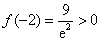 ,所以
,所以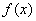 在
在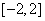 上取得最小值
上取得最小值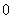 ,原命题等价于不等式
,原命题等价于不等式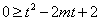 在
在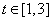 恒成立, …………………10分
恒成立, …………………10分
即: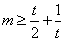 在
在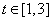 恒成立,只需
恒成立,只需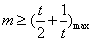 ,
,
令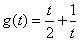 ,可得
,可得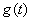 在
在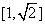 上单调递减,在
上单调递减,在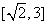 上单调递增,
上单调递增,
而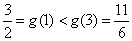 ,所以
,所以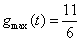 , …………………12分
, …………………12分
所以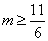 . …………………13分
. …………………13分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
已知函数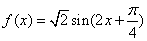 ,有下列四个结论:
,有下列四个结论:
①函数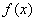 在区间
在区间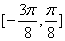 上是增函数:
上是增函数:
②点 是函数
是函数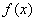 图象的一个对称中心;
图象的一个对称中心;
③函数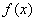 的图象可以由函数
的图象可以由函数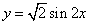 的图象向左平移
的图象向左平移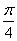 得到;
得到;
④若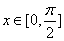 ,则函数
,则函数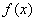 的值域为
的值域为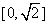 .
.
则所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
某产品的广告费用 与销售额
与销售额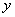 的统计数据如下表,根据下表可得回归方程
的统计数据如下表,根据下表可得回归方程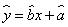 中的
中的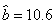 ,据此模型预报广告费用为10万元时销售额为
,据此模型预报广告费用为10万元时销售额为

A.112.1万元 B.113.1万元 C.111.9万元 D.113.9万元
查看答案和解析>>
科目:高中数学 来源: 题型:
某运输公司承担了每天至少搬运280吨水泥的任务,已知该公司有6辆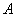 型卡车和8辆
型卡车和8辆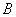 型卡车.又已知
型卡车.又已知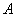 型卡车每天每辆的运载量为30吨,成本费为0.9千元;
型卡车每天每辆的运载量为30吨,成本费为0.9千元;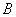 型卡车每天每辆的运载量为40吨,成本费为1千元,则该公司所花的最小成本费是 .
型卡车每天每辆的运载量为40吨,成本费为1千元,则该公司所花的最小成本费是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
为了考查两个变量x和y之间的线性关系,甲、乙两位同学各自独立做了8次和10次试验,并且利用线性回归方法,求得回归直线分别为l1,l2,已知两人得到的试验数据中,变量x和y的数据的平均值都分别相等,则下列说法正确的是 ( )
A.直线l1和l2必定重合 B.必有l1//l2
C.直线l1和l2不一定相交 D.直线l1和l2一定有公共点
查看答案和解析>>
科目:高中数学 来源: 题型:
已知矩阵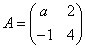 ,
,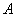 的一个特征值
的一个特征值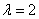 .
.
(Ⅰ)求矩阵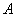 ;
;
(Ⅱ)在平面直角坐标系中,点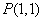 依次在矩阵
依次在矩阵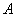 所对应的变换
所对应的变换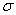 和关于
和关于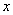 轴的反射变换
轴的反射变换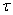 的作用下得到点
的作用下得到点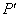 ,写出复合变换
,写出复合变换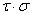 的变换公式,并求出点
的变换公式,并求出点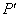 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com