Question

已知定义域为R的函数f（x）在区间（-∞，5）上单调递减，对任意实数t，都有f（5+t）=f（5-t），那么下列式子一定成立的是（ ）
A．f（-1）＜f（9）＜f（13）
B．f（13）＜f（9）＜f（-1）
C．f（9）＜f（-1）＜f（13）
D．f（13）＜f（-1）＜f（9）

Answer 1

【答案】分析：由f（5+t）=f（5-t），知函数f（x）的图象关于x=5对称，然后利用在区间（-∞，5）上单调递减，可得函数在R上的单调性，从而可得函数值的大小关系．
解答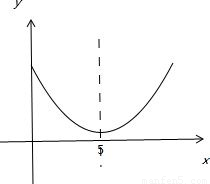：解：∵f（5+t）=f（5-t）∴函数f（x）的图象关于x=5对称
∴f（-1）=f（11），
∵函数f（x）在区间（-∞，5）上单调递减，
∴f（x）在（5，+∞）上为单调递增．
∴f（9）＜f（11）＜f（13），
即f（9）＜f（-1）＜f（13）．
故选C．
点评：本题考查了函数的单调性及单调区间，同时考查了函数图象的对称性，注意数形结合，是个基础题．