练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线C的顶点在原点，对称轴是y轴，直线与抛物线交于不同的两点、，线段中点的纵坐标为2，且.

    （1）求抛物线的标准方程；

    （2）设抛物线的焦点为，若直线经过焦点，求直线的方程.

    【答案】（1）；

    （2）；

    【解析】

    （1）根据题中所给的条件，判断出抛物线的焦点所在轴以及开口方向，从而设出抛物线的标准方程为，根据定义列出等量关系式，求得，得到抛物线的方程；

    （2）根据题意，设出直线的方程为，与抛物线的方程联立消元得到，利用题意，列出等量关系式，求得k=±，得到结果.

    （1）由题意可设抛物线C的标准方程为：，

    设，则

    ∵，∴，所以抛物线C的方程为：

    （2）由已知得k一定存在且;故可设直线的方程为：，

    则联立直线与抛物线方程，整理可得：

    由韦达定理得，∴=4解得：k=±，

    故所求直线方程为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）讨论的单调性；

    （2）若有两个不同的零点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂去年某产品的年产量为100万只，每只产品的销售价为10元，固定成本为8元今年，工厂第一次投入100万元科技成本，并计划以后每年比上一年多投入100万元科技成本，预计产量年递增10万只，第次投入后，每只产品的固定成本为为常数，且，若产品销售价保持不变，第次投入后的年利润为万元．

    （1）求的值，并求出的表达式；

    （2）问从今年算起第几年利润最高？最高利润为多少万元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题正确的是

    （1）命题“，”的否定是“，”；

    （2）l为直线，，为两个不同的平面，若，，则；

    （3）给定命题p，q，若“为真命题”，则是假命题；

    （4）“”是“”的充分不必要条件．

    A. （1）（4）B. （2）（3）C. （3）（4）D. （1）（3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线C1的参数方程为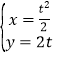（t为参数），曲线C2的参数方程为（α为参数），以O为极点，x轴的正半轴为极轴建立极坐标系．

    （1）求曲线C1和C2的极坐标方程；

    （2）直线l的极坐标方程为，直线l与曲线C1和C2分别交于不同于原点的A，B两点，求|AB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于曲线C所在平面上的定点，若存在以点为顶点的角，使得对于曲线C上的任意两个不同的点A，B恒成立，则称角为曲线C相对于点的“界角”，并称其中最小的“界角”为曲线C相对于点的“确界角”．曲线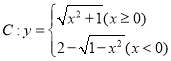相对于坐标原点的“确界角”的大小是 _________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一列非零向量满足:(其中是非零常数).

    (1)求数列的通项公式；

    (2)求向量与夹角的弧度数

    (3)当时,把中所有与共线的向量按原来的顺序排成一列,记为令为坐标原点,求点列的极限点D的坐标.(注:若点坐标为且则称点D为点列的极限点).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图：在三棱锥中，，是直角三角形，，

    ，点分别为的中点.

    （1）求证：；

    （2）求直线与平面所成角的大小；

    （3）求二面角的正切值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4—4：坐标系与参数方程

    点P是曲线C1：（x－2）2＋y2＝4上的动点，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，以极点O为中心，将点P逆时针旋转90°得到点Q，设点Q的轨迹为曲线C2．

    （Ⅰ）求曲线C1，C2的极坐标方程；

    （Ⅱ）射线（ρ＞0）与曲线C1，C2分别交于A，B两点，设定点M（2，0），求△MAB的面积．

    查看答案和解析>>

    同步练习册答案