
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直时,方程
垂直时,方程![]() 有两相异实数根,求
有两相异实数根,求![]() 的取值范围;
的取值范围;
(2)若幂函数![]() 的图象关于
的图象关于![]() 轴对称,求使不等式
轴对称,求使不等式![]() 在
在![]() 上恒成立的
上恒成立的![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)方程![]() 有两相异实数根等价于
有两相异实数根等价于![]() 有两个零点;(2)令
有两个零点;(2)令![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,即求
上恒成立,即求![]() 的最小值
的最小值![]() ,
,
![]() ,对a分类讨论研究函数的单调性,从而确定出函数的最值.
,对a分类讨论研究函数的单调性,从而确定出函数的最值.
试题解析:
(Ⅰ)由题设可得![]() ,令
,令![]() ,
,
则![]() 令
令![]() 得
得![]() ,
,
|
|
|
|
|
| 0 |
|
| 递减 | 极小值 | 递增 |
![]() ,
,
且![]() 有两个不等实根
有两个不等实根![]() 即
即![]()
![]() .
.
(Ⅱ)由题设有![]() ,令
,令![]() ,
,
则![]() ,令
,令![]() ,则
,则
![]() 又
又![]() ,
, ![]() ,
, ![]() 在
在![]() 在单调递增,
在单调递增,
又![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 内单调递增,
内单调递增, ![]() ,所以
,所以![]() .
.
②当![]() ,即
,即![]() 时,由
时,由![]() 在
在![]() 内单调递增,
内单调递增,
且![]() ,
,
![]() 使得
使得![]() ,
,
|
|
|
|
|
| 0 |
|
| 递减 | 极小值 | 递增 |
所以![]() 的最小值为
的最小值为![]() ,
,
又![]() ,所以
,所以![]()
![]() ,
,
因此,要使当![]() 时,
时, ![]() 恒成立,只需
恒成立,只需![]() ,即
,即![]() 即可.
即可.
解得![]() ,此时由
,此时由![]() ,可得
,可得![]() .
.
以下求出a的取值范围.
设![]() ,
, ![]() , 得
, 得![]() ,
,
所以![]() 在
在![]() 上单调递减,从而
上单调递减,从而![]() ,
,
综上①②所述, ![]() 的取值范围
的取值范围![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一条对称轴为
的一条对称轴为![]() ,且最高点的纵坐标是
,且最高点的纵坐标是![]() .
.
(1)求![]() 的最小值及此时函数
的最小值及此时函数![]() 的最小正周期、初相;
的最小正周期、初相;
(2)在(1)的情况下,设![]() ,求函数
,求函数![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
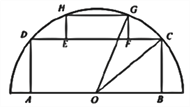
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池![]() 及其矩形附属设施
及其矩形附属设施![]() ,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为
,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形的一边
,矩形的一边![]() 在直径上,点
在直径上,点![]() 在圆周上,
在圆周上, ![]() 在边
在边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)当![]() 为何值时,能符合园林局的要求?
为何值时,能符合园林局的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
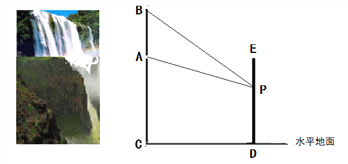
【题目】南京市江北新区计划在一个竖直长度为20米的瀑布![]() 正前方修建一座观光电梯
正前方修建一座观光电梯![]() 。如图所示,瀑布底部
。如图所示,瀑布底部![]() 距离水平地面的高度
距离水平地面的高度![]() 为60米,电梯上设有一个安全拍照口
为60米,电梯上设有一个安全拍照口![]() ,
, ![]() 上升的最大高度为60米。设
上升的最大高度为60米。设![]() 距离水平地面的高度为
距离水平地面的高度为![]() 米,
米, ![]() 处拍照瀑布的视角
处拍照瀑布的视角![]() 为
为![]() 。摄影爱好者发现,要使照片清晰,视角
。摄影爱好者发现,要使照片清晰,视角![]() 不能小于
不能小于![]() 。
。
(1)当![]() 米时,视角
米时,视角![]() 恰好为
恰好为![]() ,求电梯和山脚的水平距离
,求电梯和山脚的水平距离![]() 。
。
(2)要使电梯拍照口![]() 的高度
的高度![]() 在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离
在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com