
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且斜率大于0的直线
且斜率大于0的直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() ,
, ![]() ,直线
,直线![]() ,
, ![]() 与
与![]() 轴相交于
轴相交于![]() ,
, ![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)运用椭圆的离心率公式![]() 的关系,以及点在椭圆上,列出方程;(2)设直线
的关系,以及点在椭圆上,列出方程;(2)设直线![]() 的方程为
的方程为![]() ,联立椭圆方程,消去
,联立椭圆方程,消去![]() 得,由判别式大于零,运用韦达定理,再将
得,由判别式大于零,运用韦达定理,再将![]() 表示为关于
表示为关于![]() 的函数式,分离常数,进而可得结果.
的函数式,分离常数,进而可得结果.
试题解析:(1)![]() 椭圆
椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,
,
过点![]() ,则
,则![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,
,
直线![]() 的方程为
的方程为![]() ,可得
,可得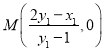 ,即
,即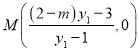 ,
,
直线![]() 的方程为
的方程为![]() ,可得
,可得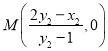 ,即
,即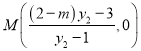 .
.
联立![]() ,消去
,消去![]() ,整理得
,整理得![]() .
.
由![]() ,可得
,可得![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
因为![]() ,
, ![]() ,所以
,所以![]() ,因此
,因此![]() ,即
,即![]() ,
,
![]() 的取值范围是
的取值范围是![]() .
.
【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求范围问题,属于难题.解决圆锥曲线中的范围问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中范围问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,单调性法求![]() 的范围的.
的范围的.


科目:高中数学 来源: 题型:
【题目】某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段![]() ,
, ![]() ,…,
,…, ![]() ,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
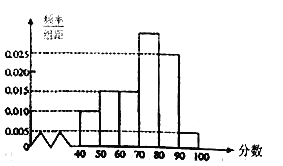
(1)估计这次考试中数学学科成绩的中位数;
(2)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组、…、第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差大于30分(以分数段为依据,不以具体学生分数为依据),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在明朝程大位《算法统宗》中,有这样的一首歌谣,叫做浮屠增级歌.“远看巍巍塔七层,红光点点倍加倍;共灯三百八十一,请问尖头几盏灯?”本题是说,“远处有一座雄伟的佛塔,塔上挂满了许多红灯,下一层灯数是上一层灯数的2倍,全塔共有381盏,试问顶层有几盏灯?”;同样在这本书中还有一道著名算题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”如果译成白话文,其意思是:“有100个和尚分100个馒头,如果大和尚一人分3个,小和尚3人分一个,正好分完.”现按照分层抽样的办法从这100名和尚中选取12人派去布置第一个问题中最顶层的灯,那么每盏灯需要分派的大小和尚数各为(A)1人,3人 (B)2人,4人 (C)3人,6人 (D)3人,9人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
喜欢 | 不喜欢 | 合计 | |
大于40岁 | 20 | 5 | 25 |
20岁至40岁 | 10 | 20 | 30 |
合计 | 30 | 25 | 55 |
(1)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设fn(x)=(3n﹣1)x2﹣x(n∈N*),An={x|fn(x)<0}
(1)定义An={x|x1<x<x2}的长度为x2﹣x1 , 求An的长度;
(2)把An的长度记作数列{an},令bn=anan+1;
1°求数列{bn}的前n项和Sn;
2°是否存在正整数m,n(1<m<n),使得S1 , Sm , Sn成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,以
,以![]() 为圆心的圆
为圆心的圆![]()
![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
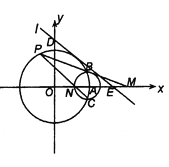
(1)若直线![]() 与圆
与圆![]() 切于第一象限,且与坐标轴交于
切于第一象限,且与坐标轴交于![]() ,当线段
,当线段![]() 长最小时,求直线
长最小时,求直线![]() 的方程;
的方程;
(2)设![]() 是圆
是圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 和
和![]() ,问
,问![]() 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=8,a4=2,且满足an+2﹣2an+1+an=0,n∈N* .
(1)求数列{an}的通项;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com