
分析 (1)由题意,函数y=f(x)是定义在R上的奇函数,x≥0时,f(x)=2x-x2,要求x<0时,f(x)的解析式,可选取x<0,得到-x>0,代入x≥0时时的解析式,得到f(-x),再由f(-x)=-f(x),两者联立,即可求得x<0时,f(x)的解析式,
(2)由题意,x>0时,g(x)=-x2+2x,分类讨论,结合g(x)的值域为[$\frac{a}{2}$,$\frac{b}{2}$],即可得出结论.
解答 解:(1)设x<0,则-x>0,
∵当x≥0时,f(x)=2x-x2,∴f(-x)=-2x-x2,
∵f(x)是定义在R上的奇函数,∴f(x)=-f(-x)=x2+2x,
∴当x<0时,f(x)=x2+2x.
(2)由题得,g(x)=-x2+2x,
当0<a<b<1时,$\left\{\begin{array}{l}{g(a)=\frac{a}{2}}\\{g(b)=\frac{b}{2}}\end{array}\right.$,解得a=b=$\frac{3}{2}$,不合题意,舍去;
当0<a<1≤b时,g(x)的最大值为g(1)=1=$\frac{b}{2}$,∴b=2,
又g(b)=g(2)=0∉[$\frac{a}{2}$,$\frac{b}{2}$],
∴b=2不合题意,舍去;
当1≤a<b时,$\left\{\begin{array}{l}{g(a)=\frac{b}{2}}\\{g(b)=\frac{a}{2}}\end{array}\right.$,无解,舍去.
综上,不存在正数a,b的值满足题意.
点评 本题考查函数最值的应用,解题的关键是理解题意,判断函数的性质,确定函数的最值,再利用函数的最值建立方程求出参数的值,利用最值建立方程是最值的一个非常重要的应用,本题第一小题求利用奇函数的性质求对称区间上的解析式,是奇函数性质的重要运用,注意总结此题的解法步骤


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由圆x2+y2=r2的面积S=πr2,推断:椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的面积S=πab; | |
| B. | 由平面三角形的性质推测空间四面体的性质; | |
| C. | 由a1=1,an=3n-2,求出S1,S2,S3,猜出数列{an}的前n项和的表达式; | |
| D. | 由于f(x)=xcosx满足f(-x)=-f(x)对?x∈R都成立,推断f(x)=xcosx为奇函数. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},+∞)$ | B. | $[{-\frac{1}{2},+∞})$ | C. | $({-∞,\frac{1}{2}}]$ | D. | $({-∞,-\frac{1}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
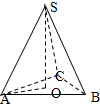 如图,在三棱锥S-ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,在三棱锥S-ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | [6,+∞) | C. | (-∞,9] | D. | (-∞,12] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com