练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．设x，y满足约束条件$\left\{\begin{array}{l}{-1≤2x+y≤1}\\{2≤x-y≤3}\end{array}\right.$，则x+y+1的最大值为1．

    分析 作出不等式组对应的平面区域，利用目标函数的几何意义，利用平移法进行求解即可．

    解答 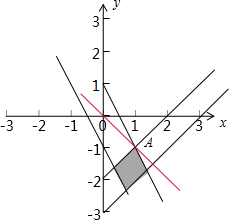解：作出x，y满足约束条件$\left\{\begin{array}{l}{-1≤2x+y≤1}\\{2≤x-y≤3}\end{array}\right.$的可行域，
    如图：$\left\{\begin{array}{l}{2x+y=1}\\{2=x-y}\end{array}\right.$解得A（1，-1），
    作出直线l：x+y+1=0，平移直线l，当它过点A（1，-1）时，
    z=x+y+1取得最大值1．
    故答案为：1．

    点评 本题主要考查线性规划的应用，根据条件结合目标函数的几何意义，利用平移法是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

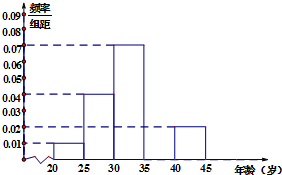    15．当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取n名市民，按年龄情况进行统计的得到频率分布表和频率分布直方图如下：
     组数分组（单位：岁）频数频率
    1 [20，25）50.05
     2[25，30）200.20
     3[30，35）a0.35
     4[35，40）30b
     5[40，45]100.10
    合计n1.00
    （1）求出表中的a，b的值，并补全频率分布直方图；
    （2）媒体记者为了做好调查工作，决定在第2，4，5组中用分层抽样的方法抽取6名市民进行问卷调查，再从这6名市民中随机抽取2名接受电视采访，求第2组至少有一名接受电视采访的概率？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．某商家在网上销售一种商品，从该商家的销售数据中抽取6天的价格与销量的对应数据，如下表所示：
    价格x（百元）456789
    销量y（件/天）908483807568
    （Ⅰ）由表中数据，看出可用线性回归模型拟合y与x的关系，试求y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，并预测当价格为1000元时，每天的商品的销量为多少；
    （Ⅱ）若以从这6天中随机抽取2天，至少有1天的价格高于700元的概率．
    参考数据：$\sum_{i=1}^{6}$xiyi=3050，$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271．
    参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{{8-{a^2}}}$=1（a＞0）的焦点在x轴上，且椭圆E的焦距为4．
    （Ⅰ）求椭圆E的标准方程；
    （Ⅱ）过椭圆外一点M（m，0）（m＞a）作倾斜角为$\frac{5π}{6}$的直线l与椭圆交于C，D两点，若椭圆E的右焦点F在以弦CD为直径的圆的内部，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

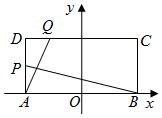    20．如图，在矩形ABCD中，|AB|=4，|AD|=2，O为AB中点，P，Q分别是AD和CD上的点，且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$，②直线AQ与BP的交点在椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）上．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）设R为椭圆E的右顶点，M为椭圆E第一象限部分上一点，作MN垂直于y轴，垂足为N，求梯形ORMN面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．如图1，在边长为2的菱形ABCD中，∠BAD=60°，将△BCD沿对角线BD折起到△B'CD的位置，使平面BC'D⊥平面ABD，E是BD的中点，FA⊥平面ABD，且FA=2$\sqrt{3}$，如图2．
    （1）求证：FA∥平面BC'D；
    （2）求平面ABD与平面FBC'所成角的余弦值；
    （3）在线段AD上是否存在一点M，使得C'M⊥平面FBC？若存在，求$\frac{AM}{AD}$的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．某市对大学生毕业后自主创业人员给予小额贷款补贴，贷款期限分为6个月、12个月、18个月、24个月、36个月五种，对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元，从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计，选取贷款期限的频数如表：
     贷款期限  6个月  12个月  18个月  24个月  36个月
     频数 20 40 20 10 10
    （Ⅰ）若小王准备申请此项贷款，求其获得政府补贴不超过300元的概率（以上表中各项贷款期限的频率作为2017年自主创业人员选择各种贷款期限的概率）；
    （Ⅱ）若小王和小李同时申请此项贷款，求两人所获得政府补贴之和不超过600元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

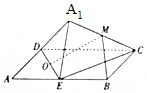    14．如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE（A1∉平面ABCD），若M、O分别为线段A1C、DE的中点，则在△ADE翻转过程中，下列说法错误的是（　　）
    A．与平面A1DE垂直的直线必与直线BM垂直
    B．异面直线BM与A1E所成角是定值
    C．一定存在某个位置，使DE⊥MO
    D．三棱锥A1-ADE外接球半径与棱AD的长之比为定值

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=2|x-2|+3|x+3|．
    （1）解不等式：f（x）＞15；
    （2）若函数f（x）的最小值为m，正实数a，b满足4a+25b=m，证明：$\frac{1}{a}$+$\frac{1}{b}$≥$\frac{49}{10}$．

    查看答案和解析>>

    同步练习册答案