
(本题满分10分)已知从“神州”飞船带回的某种植物种子每粒成功发芽的概率都为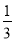 ,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
(1)求随机变量ξ的数学期望E(ξ);
(2)记“函数f(x)= x2-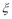 x-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率P(A).
x-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率P(A).
(1)由题意知:ξ的可能取值为0,2,4.
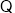 “
“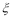 =0”指的是实验成功2次 ,失败2次;
=0”指的是实验成功2次 ,失败2次; .
.
 “ξ=2”指的是实验成功3次 ,失败1次或实验成功1次 ,失败3次;
“ξ=2”指的是实验成功3次 ,失败1次或实验成功1次 ,失败3次;

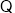 “
“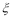 =4”指的是实验成功4次 ,失败0次或实验成功0次 ,失败4次;
=4”指的是实验成功4次 ,失败0次或实验成功0次 ,失败4次;
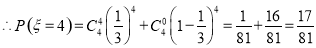 .
. .故随机变量ξ的数学期望E(ξ)为
.故随机变量ξ的数学期望E(ξ)为 . 6分
. 6分
(2)由题意知:f(2)f(3)=(3-2 )(8-3
)(8-3 )
) ,故
,故 .
.
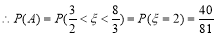 ,故事件A发生的概率P(A)为
,故事件A发生的概率P(A)为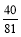 . 10分
. 10分
【解析】
试题分析:(1)由题意知ξ的可能取值为0,2,4,结合变量对应的事件,用等可能事件的概率公式做出结果,写出分布列和期望.(2)由题意知:f(2)f(3)=(3-2 )(8-3
)(8-3 )
) ,故
,故 ,(2)由题意知:f(2)f(3)=(3-2
,(2)由题意知:f(2)f(3)=(3-2 )(8-3
)(8-3 )
) ,故
,故 即求P(2)的值
即求P(2)的值
考点:离散型随机变量的期望与方差;等可能事件的概率;离散型随机变量及其分布列
点评:本题考查离散型随机变量的分布列和期望,考查等可能事件的概率,是一个综合题,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题.


科目:高中数学 来源:2014-2015学年广东省肇庆市高二上学期期末考试理科数学试卷(解析版) 题型:选择题
已知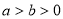 ,椭圆
,椭圆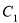 的方程为
的方程为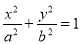 ,双曲线
,双曲线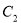 的方程为
的方程为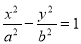 ,
,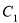 与
与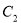 的离心率之积为
的离心率之积为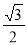 ,则
,则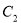 的渐近线方程为
的渐近线方程为
A.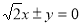 B.
B.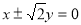 C.
C.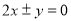 D.
D.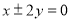
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省天水市高三一轮复习基础知识检测文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—5:不等式选讲
设函数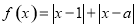 .
.
(1)若 时,解不等式
时,解不等式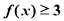 ;
;
(2)如果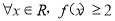 ,求
,求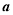 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省天水市高三一轮复习基础知识检测文科数学试卷(解析版) 题型:解答题
(本小题满分10分)从某校高三年级800名学生中随机抽取50名测量身高.据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果分成八组得到的频率分布直方图如下:

(1)试估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为多少;
(2)在样本中,若学校决定身高在185cm以上的学生中随机抽取2名学生接受某军校考官进行 面试,求:身高在190cm以上的学生中至少有一名学生接受面试的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期第三次月考数学试卷(解析版) 题型:解答题
(本小题满分12分,(1)小问3分,(2)小问4分,(3)小问5分)
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个 都成立,则称函数
都成立,则称函数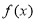 是“(
是“( )型函数”.
)型函数”.
(1)判断函数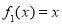 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(2)若函数 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对 ;
;
(3)已知函数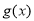 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对 为(1,4).当
为(1,4).当 时,
时,

 ,若当
,若当 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期第三次月考理科数学试卷(解析版) 题型:选择题
下列五个命题:
①若xy=0,则x=0且y=0”的逆否命题;
②正方形是菱形”的否命题;
③若 ”的逆命题;
”的逆命题;
④“m>2, ”;
”;
⑤命题p:“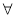
 ,
, ≥0”的否定是命题q:“
≥0”的否定是命题q:“
 ,
, ”,且命题q为假命题.
”,且命题q为假命题.
其中真命题的个数为( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com