
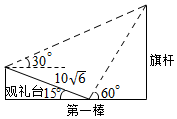
 如图,在坡角(坡面与水平面的夹角)为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°,且第一排和最后一排的距离10$\sqrt{6}$米,则旗杆的高度为30米.
如图,在坡角(坡面与水平面的夹角)为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°,且第一排和最后一排的距离10$\sqrt{6}$米,则旗杆的高度为30米. 分析 求出△ACD的各角,利用正弦定理解出AD,则AB=ADsin60°.
解答 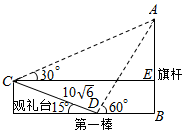 解由已知得∠ACD=30°+15°=45°,∠ADC=180°-60°-15°=105°,∴∠CAD=30°.
解由已知得∠ACD=30°+15°=45°,∠ADC=180°-60°-15°=105°,∴∠CAD=30°.
在△ACD中,由正弦定理得$\frac{CD}{sin∠CAD}=\frac{AD}{sin∠ACD}$,
即$\frac{10\sqrt{6}}{\frac{1}{2}}=\frac{AD}{\frac{\sqrt{2}}{2}}$,解得AD=20$\sqrt{3}$.
∴AB=AD•sin∠ADB=20$\sqrt{3}×\frac{\sqrt{3}}{2}$=30(米)
故答案为:30.
点评 本题考查了正弦定理在解三角形中的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
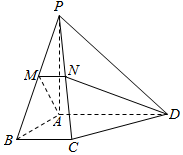 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(-1,+∞) | B. | (-∞,-2)∪[-1,+∞) | C. | [-2,-1) | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日需求量x | (0,400] | (400,600] | (600,800] | (800,1000] |
| 频率 | 0.2 | 0.4 | 0.3 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,$\frac{4}{3}$) | B. | [$\frac{4}{3}$,4] | C. | [$\frac{4}{3}$,3) | D. | [$\frac{1}{2}$,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com