
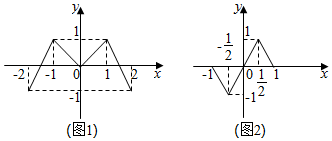 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,若f(y0)=0且y0=g(x0),则x0的值为-1,0,或1.
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,若f(y0)=0且y0=g(x0),则x0的值为-1,0,或1. 科目:高中数学 来源: 题型:填空题
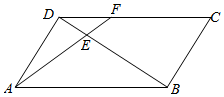 如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.
如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
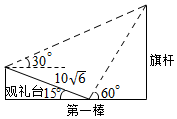 如图,在坡角(坡面与水平面的夹角)为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°,且第一排和最后一排的距离10$\sqrt{6}$米,则旗杆的高度为30米.
如图,在坡角(坡面与水平面的夹角)为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°,且第一排和最后一排的距离10$\sqrt{6}$米,则旗杆的高度为30米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 期末分数段 | (0,60) | [60,75) | [75,90) | [90,105) | [105,120) | [120,150] |
| 人数 | 5 | 10 | 15 | 10 | 5 | 5 |
| “过关”人数 | 1 | 2 | 9 | 7 | 3 | 4 |
| 分数低于90分人数 | 分数不低于90分人数 | 合计 | |
| 过关人数 | |||
| 不过关人数 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| K | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
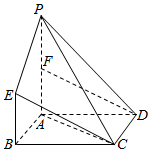 如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.
如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 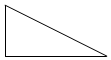 | B. | 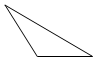 | C. | 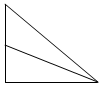 | D. | 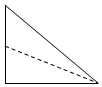 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 50 | 200 | 350 | 300 | 100 |
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 250 | 300 | 150 | 100 | 200 |
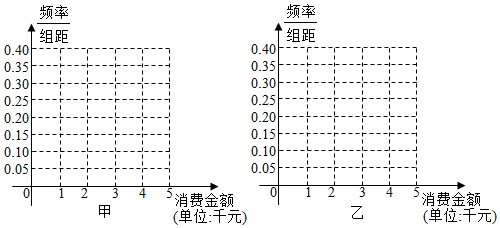
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com