
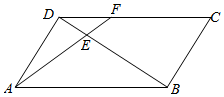
 如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.
如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$. 分析 根据△DEF∽△BEA得出$\overrightarrow{DF}$与$\overrightarrow{AB}$的数量关系,用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{AF}$进行计算.
解答 解:∵△DEF∽△BEA,
∴$\frac{DF}{AB}=\frac{DE}{BE}=\frac{1}{3}$,
∴$\overrightarrow{AF}=\overrightarrow{AD}+\frac{1}{3}\overrightarrow{AB}$.
∴$\overrightarrow{AF}•\overrightarrow{AD}$=($\overrightarrow{AD}+\frac{1}{3}\overrightarrow{AB}$)$•\overrightarrow{AD}$=${\overrightarrow{AD}}^{2}$+$\frac{1}{3}$$\overrightarrow{AB}•\overrightarrow{AD}$=1+$\frac{1}{3}×2×1×cos$60°=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了平面向量的数量积运算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
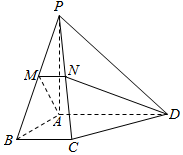 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com