
分析 (1)取AB中点D,连结CD,取CD中点M,连结EM,BM,推导出∠BEM是异面直线PD与BE所成角,由此能求出异面直线PD与BE所成角的余弦值.
(2)过P作PO⊥平面ABC,O是垂足,过E作EF⊥平面ABC,F是垂足,∠EBF是BE与平面ABC所成角,由此能求出BE与平面ABC所成角的正弦值.
解答 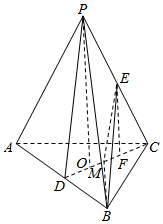 解:(1)取AB中点D,连结CD,取CD中点M,连结EM,BM,
解:(1)取AB中点D,连结CD,取CD中点M,连结EM,BM,
∵正三棱锥P-ABC中,底面边长等于1,侧棱PA=$\sqrt{2}$,D,E分别为AB,PC中点,
∴EM∥PD,∴∠BEM是异面直线PD与BE所成角,
由题意得PD=$\sqrt{2-\frac{1}{4}}$=$\frac{\sqrt{7}}{2}$,CD=$\sqrt{1-\frac{1}{4}}$=$\frac{\sqrt{3}}{2}$,EM=$\frac{1}{2}PD=\frac{\sqrt{7}}{4}$,
cos∠BPE=$\frac{2+2-1}{2×\sqrt{2}×\sqrt{2}}$=$\frac{3}{4}$=$\frac{2+\frac{1}{4}-B{E}^{2}}{2×\sqrt{2}×\frac{\sqrt{2}}{2}}$,解得BE=$\frac{\sqrt{3}}{2}$,
BM=$\sqrt{B{D}^{2}+(\frac{CD}{2})^{2}}$=$\sqrt{\frac{1}{4}+\frac{3}{16}}$=$\frac{\sqrt{7}}{4}$,
∴cos∠BEM=$\frac{B{E}^{2}+M{E}^{2}-B{M}^{2}}{2×BE×EM}$=$\frac{\frac{3}{4}+\frac{7}{16}-\frac{7}{16}}{2×\frac{\sqrt{3}}{2}×\frac{\sqrt{7}}{4}}$=$\frac{\sqrt{21}}{7}$,
∴异面直线PD与BE所成角的余弦值为$\frac{\sqrt{21}}{7}$.
(2)过P作PO⊥平面ABC,O是垂足,过E作EF⊥平面ABC,F是垂足,
则∠EBF是BE与平面ABC所成角,
OD=$\frac{1}{3}CD=\frac{\sqrt{3}}{6}$,PO=$\sqrt{P{D}^{2}-O{D}^{2}}$=$\sqrt{\frac{7}{4}-\frac{1}{12}}$=$\frac{\sqrt{15}}{3}$,EF=$\frac{1}{2}PO=\frac{\sqrt{15}}{6}$,
∴sin∠EBF=$\frac{EF}{BE}$=$\frac{\frac{\sqrt{15}}{6}}{\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{5}}{3}$.
∴BE与平面ABC所成角的正弦值为$\frac{\sqrt{5}}{3}$.
点评 本题考查异面直线所成角的余弦值的求法,考查正弦直线所成角的正弦值的求法,是中档题,解题时要认真审题,注意空让思维能力的培养.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4+\sqrt{2}}{7}$ | B. | $\frac{4-\sqrt{2}}{7}$ | C. | $\frac{4+\sqrt{2}}{8}$ | D. | $\frac{4-\sqrt{2}}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)=cos(2x+$\frac{π}{3}$) | B. | g(x)=cos(2x+$\frac{π}{6}$) | C. | g(x)=cos($\frac{x}{2}$+$\frac{π}{3}$) | D. | g(x)=cos($\frac{x}{2}$+$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
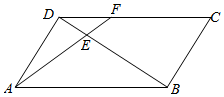 如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.
如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com