
| A. | $\frac{4+\sqrt{2}}{7}$ | B. | $\frac{4-\sqrt{2}}{7}$ | C. | $\frac{4+\sqrt{2}}{8}$ | D. | $\frac{4-\sqrt{2}}{8}$ |
分析 根据几何概型的概率公式进行转化求解即可.
解答  解:∵AD=CD=$\frac{1}{2}$AB=1,
解:∵AD=CD=$\frac{1}{2}$AB=1,
∴AC=$\sqrt{2}$,AB=2,
若AM≥$\sqrt{2}$,则M位于线段CB,和BF上,
则BC+BF=$\sqrt{2}$+2-$\sqrt{2}$=2,
梯形的周长l=1+1+2+$\sqrt{2}$=4+$\sqrt{2}$,
则对应的概率P=$\frac{2}{4+\sqrt{2}}=\frac{2(4-\sqrt{2})}{(4+\sqrt{2})(4-\sqrt{2})}$=$\frac{2(4-\sqrt{2})}{14}$=$\frac{4-\sqrt{2}}{7}$,
故选:B.
点评 本题主要考查几何概型的概率的计算,根据条件转化为长度之间的关系是解决本题的关键.


科目:高中数学 来源: 题型:选择题
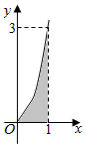 已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )
已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为39,由此可估计$\int\begin{array}{l}1\\ 0\end{array}f(x)dx$的值约为( )| A. | $\frac{61}{100}$ | B. | $\frac{39}{100}$ | C. | $\frac{10}{100}$ | D. | $\frac{117}{100}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
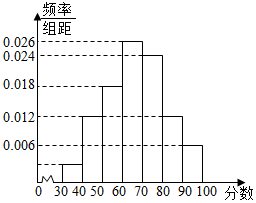 某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b= | |
| 女生 | c= | d=34 | |
| 合计 | n=100 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com