练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知全集U=R，集合A={x|-2≤x＜0}，B={x|2x-1＜$\frac{1}{4}$}，则A∩B=（　　）
    A．（-∞，-2）∪（-1，+∞）B．（-∞，-2）∪[-1，+∞）C．[-2，-1）D．（-2，+∞）

    分析 求出B中不等式的解集确定出B，找出A与B的交集即可．

    解答 解：由B中不等式变形得：2x-1＜$\frac{1}{4}$=2-2，得到x-1＜-2，
    解得：x＜-1，即B=（-∞，-1），
    ∵A=[-2，0），
    ∴A∩B=[-2，-1），
    故选：C．

    点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．已知函数f（x）=ax+m（a∈R）所表示的直线的纵截距为-1，函数g（x）=lnx+f（x）+n且g（1）=f′（1）．若命题“?x0∈（0，+∞），使得f（x0）g（x0）＜0”为假命题，则实数a的取值范围为a=e或a≤-$\frac{1}{e}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．若$\frac{1-tanθ}{1+tanθ}$=3-2$\sqrt{2}$，求$\frac{（sinθ+cosθ）^{2}-1}{cotθ-sinθ•cosθ}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．掷两枚骰子，则向上的点数之和小于6的概率为$\frac{5}{18}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

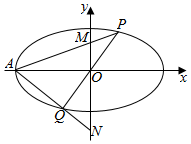    14．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$离心率$e=\frac{{\sqrt{3}}}{2}$，短轴长为2．
    （Ⅰ）求椭圆C的标准方程；
    （Ⅱ） 设直线l过椭圆C的右焦点，并与椭圆相交于E，F两点，截得的弦长为$\frac{5}{2}$，求直线l的方程；
    （Ⅲ） 如图，椭圆左顶点为A，过原点O的直线（与坐标轴不重合）与椭圆C交于P，Q两点，直线PA，QA分别与y轴交于M，N两点．试问：以MN为直径的圆是否经过定点（与直线PQ的斜率无关）？请证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

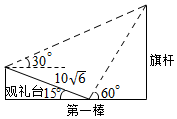    4．如图，在坡角（坡面与水平面的夹角）为15°的观礼台上，某一列座位与旗杆在同一个垂直于地面的平面上，在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°，且第一排和最后一排的距离10$\sqrt{6}$米，则旗杆的高度为30米．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

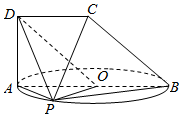    11．如图，梯形ABCD所在平面与以AB为直径的圆所在平面垂直，O为圆心，AB∥CD，∠BAD=90°，AB=2CD．若点P是⊙O上不同于A，B的任意一点．
    （Ⅰ）求证：BP⊥平面APD；
    （Ⅱ）设平面BPC与平面OPD的交线为直线l，判断直线BC与直线l的位置关系，并加以证明；
    （Ⅲ）求几何体DOPA与几何体DCBPO的体积之比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

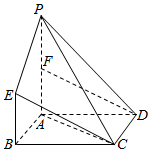    8．如图，矩形ABCD中，BC=2，AB=1，PA⊥平面ABCD，BE∥PA，BE=$\frac{1}{2}$PA，F为PA的中点．
    （1）求证：PC∥平面BDF．
    （2）记四棱锥C-PABE的体积为V1，三棱锥P-ACD的体积为V2，求$\frac{V_1}{V_2}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若函数f（x）=ln（x+$\sqrt{a+{x}^{2}}$）为奇函数，则a=（　　）
    A．-1B．0C．1D．-1或1

    查看答案和解析>>

    同步练习册答案