
剖析:求函数的单调区间(亦即判断函数的单调性),一般有三种方法:
(1)图象法;(2)定义法;(3)利用已知函数的单调性.但本题图象不易作,利用y=x与y=![]() 的单调性(一增一减)也难以确定,故只有用单调性定义来确定,即判断f(x2)-f(x1)的正负.
的单调性(一增一减)也难以确定,故只有用单调性定义来确定,即判断f(x2)-f(x1)的正负.
解:首先确定定义域:{x|x≠0},
∴在(-∞,0)和(0,+∞)两个区间上分别讨论.任取x1、x2∈(0,+∞)且x1<x2,则f(x2)-f(x1)=x2+![]() -x1-
-x1-![]() =(x2-x1)+
=(x2-x1)+![]() =(x2-x1)(1-
=(x2-x1)(1-![]() ),要确定此式的正负只要确定1-
),要确定此式的正负只要确定1-![]() 的正负即可.
的正负即可.
这样,又需要判断![]() 大于1,还是小于1.由于x1、x2的任意性,考虑到要将(0,+∞)分为(0,1)与(1,+∞)(这是本题的关键).
大于1,还是小于1.由于x1、x2的任意性,考虑到要将(0,+∞)分为(0,1)与(1,+∞)(这是本题的关键).
(1)当x1、x2∈(0,1)时,1-![]() <0,
<0,
∴f(x2)-f(x1)<0为减函数.
(2)当x1、x2∈(1,+∞)时,1-![]() >0,
>0,
∴f(x2)-f(x1)>0为增函数.
同理可求(3)当x1、x2∈(-1,0)时,为减函数;(4)当x1、x2∈(-∞,-1)时,为增函数.
讲评:解答本题易出现以下错误结论:f(x)在(-1,0)∪(0,1)上是减函数,在(-∞,-1)∪(1,+∞)上是增函数,或说f(x)在(-∞,0)∪(0,+∞)上是单调函数.避免错误的关键是要正确理解函数的单调性概念:函数的单调性是对某个区间而言的,而不是两个或两个以上不相交区间的并.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014届辽宁省丹东市高二上学期期末考试文数试卷(解析版) 题型:解答题
(本小题满分12分)已知函数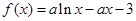 (a∈R且
(a∈R且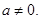 ).
).
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意t∈[1,2],函数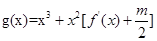 在区间(t,3)上总不是单调函数,求m的取值范围.
在区间(t,3)上总不是单调函数,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源:新课标高三数学导数专项训练(河北) 题型:解答题
设a为实常数,函数f(x)=-x3+ax2-4.
(1)若函数y=f(x)的图象在点P(1,f(1))处的切线的倾斜角为,求函数f(x)的单调区间;
(2)若存在x0∈(0,+∞),使f(x0)>0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012年广东省高二12月月考理科数学 题型:解答题
.已知函数f(x)=(x2+ax-2a2+3a)ex(x∈R),其中a∈R.
(Ⅰ)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线的斜率;
(Ⅱ)当 时,求函数f(x)的单调区间与极值.
时,求函数f(x)的单调区间与极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com