
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:

由散点图可知,销售量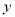 与价格
与价格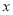 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;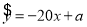
(1)求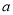 的值;
的值;
(2)预计在今后的销售中,销量与单价仍然服从线性回归直线方程中的关系,且该产品的成本是每件4元,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入一成本)
科目:高中数学 来源:2015届河南长葛第三实验高中高二下学期第一次考试文数学卷(解析版) 题型:选择题
用演绎法证明函数 是增函数时的小前提是
是增函数时的小前提是
A.增函数的定义
B.函数 满足增函数的定义
满足增函数的定义
C.若 ,则
,则
D.若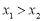 ,则
,则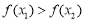
查看答案和解析>>
科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试理科试卷(A卷)(解析版) 题型:选择题
已知向量 ,
,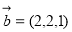 ,则以
,则以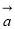 ,
, 为邻边的平行四边形的面积为( )
为邻边的平行四边形的面积为( )
A.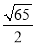 B.
B.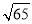 C.4 D.8
C.4 D.8
查看答案和解析>>
科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试理科数学试卷(A)(解析版) 题型:解答题
已知 是函数
是函数 的一个极值点,其中
的一个极值点,其中 .
.
(1) 与
与 的关系式;
的关系式;
(2)求 的单调区间;
的单调区间;
(3)当 时,函数
时,函数 的图象上任意一点处的切线的斜率恒大于
的图象上任意一点处的切线的斜率恒大于 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试理科数学试卷(A)(解析版) 题型:选择题
设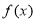 ,
,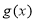 分别是定义在
分别是定义在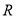 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时,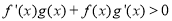 ,且
,且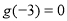 ,则不等式
,则不等式 的解集是 ( )
的解集是 ( )
A. B.
B.
C.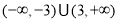 D.
D.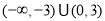
查看答案和解析>>
科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试文科试卷(A卷)(解析版) 题型:选择题
设 ,
, 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是 ( )
的解集是 ( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com