
分析 (1)令x=-1,y=1,利用f(x+y)-f(y)=x(x+2y+1),即可求得f(0)的值;
(2)令y=0,则f(x)-f(0)=x(x+1),结合f(0)=-2,可求f(x)的解析式;
(3)根据题意,将f(x)+3<2x+a变形可得x2-x+1<a,分析x2-x+1的最大值,可得a的范围,即集合A;由(2)可得g(x)的解析式,结合二次函数的性质可得b的取值范围,即可得集合B,进而可得CRB;从而可求A∩CRB.
解答 解:(1)根据题意,在f(x+y)-f(y)=x(x+2y+1)中,
令x=-1,y=1,可得f(0)-f(1)=-1(-1+2+1),
又由f(1)=0,则有f(0)=-2;
(2)在f(x+y)-f(y)=x(x+2y+1)中,
令y=0,则f(x)-f(0)=x(x+1)
又由f(0)=-2,则f(x)=x2+x-2;
(3)不等式f(x)+3<2x+a,等价于x2+x-2+3<2x+a,即x2-x+1<a,
若不等式f(x)+3<2x+a恒成立,则有x2-x+1<a恒成立,
又由$0<x<\frac{1}{2}$,则$\frac{3}{4}$<x2-x+1<1,必有a>1;
故A={a|a≥1};
g(x)=x2+x-2-ax=x2+(1-a)x-2,
若g(x)在[-2,2]上是单调函数,必有$\frac{a-1}{2}$≤-2或$\frac{a-1}{2}$≥2成立,
解可得a≤-3,或a≥5.
故B={a|a≤-3,或a≥5},则CRB={a|-3<a<5}
故A∩CRB={a|1≤a<5}.
点评 本题考查抽象函数的运用,涉及二次函数的性质,此类问题一般用特殊值法分析,解题的关键是利用二次函数的性质化简集合A,B.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a•3=b•3,则a=b类比推出 若a•0=b•0,则a=b | |
| B. | 若(a+b)c=ac+bc类比推出 $\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$(c≠0) | |
| C. | 若(a+b)c=ac+bc类比推出 (a•b)c=ac•bc | |
| D. | 若(ab)n=anbn类比推出 (a+b)n=an+bn |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{3}$,0) | B. | ( $\frac{π}{4}$,0) | C. | (-$\frac{π}{12}$,0) | D. | ($\frac{π}{2}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
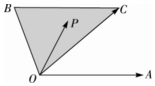 已知图中∠AOC+2∠BOC=π,|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,P为图中的阴影中(含边界)任意点,并且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$,下列正确的是①③⑤
已知图中∠AOC+2∠BOC=π,|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,P为图中的阴影中(含边界)任意点,并且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$,下列正确的是①③⑤查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com