
分析 利用函数的性质验证命题的真假即可.
解答 解:当f(x)=${(\frac{3}{2})}^{x}$时,
①f(x1+x2)=$(\frac{3}{2})^{{x}_{1}+{x}_{2}}$=$(\frac{3}{2})^{{x}_{1}}•(\frac{3}{2})^{{x}_{2}}$=f(x1)•f(x2),①正确;
②f(x1•x2)=$(\frac{3}{2})^{{x}_{1}{x}_{2}}$≠f(x1)+f(x2),不正确;
③f($\frac{{x}_{1}{+x}_{2}}{2}$)>$\frac{f{(x}_{1})+f{(x}_{2})}{2}$,说明函数是凸函数,而f(x)=${(\frac{3}{2})}^{x}$是凹函数,所以不正确;
④$\frac{f{(x}_{1})-f{(x}_{2})}{{x}_{1}{-x}_{2}}$>0,说明函数是增函数,而f(x)=${(\frac{3}{2})}^{x}$是增函数,所以正确;
⑤当1<x1<x2时$\frac{f{(x}_{1})}{{x}_{1}-1}>\frac{f{(x}_{2})}{{x}_{2}-1}$.说明函数与(1,0)连线的斜率在减少,所以正确;
故答案为①④⑤.
点评 本题考查函数的基本性质的应用,考查命题的真假的判断,是基础题.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
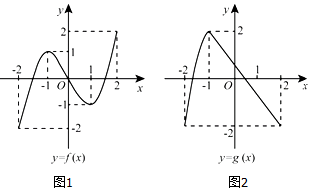
| A. | 函数f[g(x)]的零点有且仅有6个 | B. | 函数g[f(x)]的零点有且仅有3个 | ||
| C. | 函数f[f(x)]的零点有且仅有5个 | D. | 函数g[g(x)]的零点有且仅有4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com