
分析 (1)由题意知,各局比赛结果相互独立,求出对应的概率值即可;
(2)由题意知,随机变量X的所有可能的取值,根据事件的互斥性计算概率值,从而写出X的分布列.
解答 解:(1)记“甲队以3:0胜利”为事件A1,
“甲队以3:1胜利”为事件A2,
“甲队以3:2胜利”为事件A3,
由题意知,各局比赛结果相互独立,
所以P(A1)=${(\frac{2}{3})}^{3}$=$\frac{8}{27}$,
P(A2)=${C}_{3}^{2}$•${(\frac{2}{3})}^{2}$•(1-$\frac{2}{3}$)•$\frac{2}{3}$=$\frac{8}{27}$,
P(A3)=${C}_{4}^{2}$•${(\frac{2}{3})}^{2}$•${(1-\frac{2}{3})}^{2}$•$\frac{1}{2}$=$\frac{4}{27}$;
所以甲队以3:0胜利、以3:1胜利的概率都为$\frac{8}{27}$,
以3:2胜利的概率为$\frac{4}{27}$;
(2)设“乙队以3:2胜利”为事件A4,
由题意知,各局比赛结果相互独立,
所以P(A4)=${C}_{4}^{2}$•${(1-\frac{2}{3})}^{2}$•${(\frac{2}{3})}^{2}$•(1-$\frac{1}{2}$)=$\frac{4}{27}$;
由题意知,随机变量X的所有可能的取值为0,1,2,3,
根据事件的互斥性得
P(X=0)=P(A1+A2)=P(A1)+P(A2)=$\frac{16}{27}$;
又P(X=1)=P(A3)=$\frac{4}{27}$,
P(X=2)=P(A4)=$\frac{4}{27}$,
P(X=3)=1-P(X=0)-P(X=1)-P(X=2)=$\frac{3}{27}$,
故X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{16}{27}$ | $\frac{4}{27}$ | $\frac{4}{27}$ | $\frac{3}{27}$ |
点评 本题考查了相互独立性事件的概率计算与分布列问题,是综合题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{3}$,0) | B. | ( $\frac{π}{4}$,0) | C. | (-$\frac{π}{12}$,0) | D. | ($\frac{π}{2}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.
如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-1] | B. | (1,2) | C. | [-2,-1)∪(1,2] | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
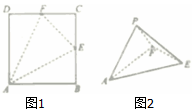 如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )
如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )| A. | $\sqrt{6}π$ | B. | 6π | C. | $4\sqrt{3}π$ | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com