
 如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.
如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.分析 (Ⅰ)在△DBC中,由正弦定理得:$\frac{BC}{sin∠CDB}=\frac{BD}{sin∠BCD}$,在△ACD中,由正弦定理得$\frac{AC}{sin∠CDA}=\frac{AD}{sin∠ACD}$,
sin∠ADC=sin∠BDC,AD=DB,AC=2BC,得sin∠BCD=2sin∠ACD;
(Ⅱ)由sin∠BCD=2sin∠ACD=1,得∠BCD=90°,∠ACB=120°,
在△ABC中由余弦定理求得AB
解答 解:(Ⅰ)在△DBC中,由正弦定理得:$\frac{BC}{sin∠CDB}=\frac{BD}{sin∠BCD}$,在△ACD中,由正弦定理得$\frac{AC}{sin∠CDA}=\frac{AD}{sin∠ACD}$,
即BCsin∠BCD=DBsin∠CBD,ACsin∠ACD=ADsin∠CDA.
∵sin∠ADC=sin∠BDC
又∵CD是AB边上的中线且AC=2BC,∴sin∠BCD=2sin∠ACD;
(Ⅱ)∵∠ACD=30°,由(Ⅰ)sin∠BCD=2sin∠ACD=1,即∠BCD=90°,∴∠ACB=120°,
由余弦定理$AB=\sqrt{A{C^2}+B{C^2}-2AC•BCcos∠ACB}=\sqrt{4+1+2}=\sqrt{7}$.
点评 本题考查了正余弦定理在解三角形中的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
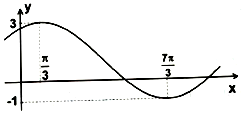 已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象.
已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,六棱锥P-ABCDEF的底面是边长为1的正六边形,PA⊥底面ABCDEF.
如图,六棱锥P-ABCDEF的底面是边长为1的正六边形,PA⊥底面ABCDEF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
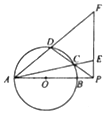 如图,AB是圆O的直径,P是线段AB延长线上一点,割线PCD交圆O于点C,D,过点P作AP的垂线,交线段AC的延长线于点E,交线段AD的延长线于点F,且PE•PF=5,PB=$\frac{1}{2}$OA.
如图,AB是圆O的直径,P是线段AB延长线上一点,割线PCD交圆O于点C,D,过点P作AP的垂线,交线段AC的延长线于点E,交线段AD的延长线于点F,且PE•PF=5,PB=$\frac{1}{2}$OA.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com