
 已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象.
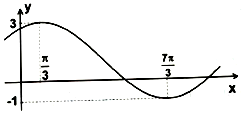
已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象.分析 (1)由图象列出方程组求出m、n的值,由周期公式求出ω的值,把点$(\frac{π}{3},3)$代入解析式求出φ的值,即可求出f(x);
(2)由(1)化简$f(A)=1+\sqrt{3}$后,由内角的范围和特殊角的三角函数值求出A,由条件和正弦定理求出b、c,表示出△ABC的周长,由整体思想和正弦函数的性质求出△ABC的周长的取值范围.
解答 解:(1)由图得,$\left\{\begin{array}{l}{m+n=3}\\{-m+n=-1}\end{array}\right.$,解得m=2、n=1,
且 $\frac{1}{2}T=\frac{7π}{3}-\frac{π}{3}$=2π,则T=4π,
由$\frac{2π}{ω}=4π$得$ω=\frac{1}{2}$,
因为过点$(\frac{π}{3},3)$,所以$2sin(\frac{1}{2}×\frac{π}{3}+φ)+1=3$,
即$sin(\frac{π}{6}+φ)=1$,所以φ=$\frac{π}{3}$,
则$f(x)=2sin({\frac{1}{2}x+\frac{π}{3}})+1$;
(2)由(1)得,$f(A)=2sin({\frac{1}{2}A+\frac{π}{3}})+1=1+\sqrt{3}$,
化简得,$sin({\frac{1}{2}A+\frac{π}{3}})=\frac{{\sqrt{3}}}{2}$,
由0<A<π得,$\frac{1}{2}A+\frac{π}{3}∈({\frac{π}{3},\frac{5π}{6}})$,
则$\frac{1}{2}A+\frac{π}{3}=\frac{2π}{3}$,所以$A=\frac{2π}{3}$,
由正弦定理得,$\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA}=\frac{{\sqrt{3}}}{{\frac{{\sqrt{3}}}{2}}}=2$,
则b=2sinB,c=2sinC,
所以周长为$\sqrt{3}+2sinB+2sinC$=$\sqrt{3}+2sinB+2sin(\frac{π}{3}-B)$
=$\sqrt{3}+2(sinB+\frac{\sqrt{3}}{2}cosB-\frac{1}{2}sinB)$
=$\sqrt{3}+2sin({B+\frac{π}{3}})$,
又$A=\frac{2π}{3}$,则$0<B<\frac{π}{3}$,即$B+\frac{π}{3}∈({\frac{π}{3},\frac{2π}{3}})$,
所以$sin({B+\frac{π}{3}})∈({\frac{{\sqrt{3}}}{2},1}]$,
则周长范围是$({2\sqrt{3},2+\sqrt{3}}]$.
点评 本题考查正弦定理,由图象求三角形的解析式,周期公式,以及正弦函数的性质的应用,考查化简、变形能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分不必要条件 | D. | 必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{3}$π | B. | $\frac{28}{3}$π | C. | $\frac{28\sqrt{21}}{27}$π | D. | $\frac{25\sqrt{21}}{27}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 该推理是正确的 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.
如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
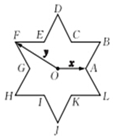 将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.
将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com