
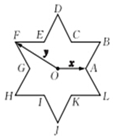
 将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.
将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5. 分析 根据题意,画出图形,结合图形,得出求a+b的最大值时﹐只需考虑图中6个顶点的向量即可,分别求出即得结论.
解答 解:欲求a+b的最大值﹐只需考虑右图中6个顶点的向量即可,讨论如下﹔
(1)∵$\overrightarrow{OA}$═$\overrightarrow{x}$﹐∴(a,b)=(1,0);
(2)∵$\overrightarrow{OB}=\overrightarrow{OF}+\overrightarrow{FB}=\overrightarrow{y}+3\overrightarrow{x}$,所以(a,b)=(3,1);
(3)∵$\overrightarrow{OC}=\overrightarrow{OF}+\overrightarrow{FC}=\overrightarrow{\\;y}+2\overrightarrow{x}$,所以(a,b)=(2,1);
(4)∵$\overrightarrow{OD}=\overrightarrow{OF}+\overrightarrow{FE}+\overrightarrow{ED}=3\overrightarrow{x}+2\overrightarrow{y}$,所以(a,b)=(3,2);
(5)∵$\overrightarrow{OE}=\overrightarrow{OF}+\overrightarrow{FE}=\overrightarrow{x}+\overrightarrow{y}$,所以(a,b)=(1,1);
(6)∵$\overrightarrow{OF}=\overrightarrow{y}$,所以(a,b)=(0,1);
因此﹐a+b的最大值为3+2=5﹒
故答案为:5﹒
点评 本题考查了平面向量的基本定理的应用问题,也考查了平面向量的坐标表示的应用问题,属于中档题.


科目:高中数学 来源: 题型:解答题
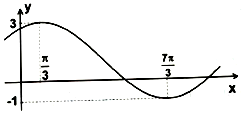 已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象.
已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l丄α,l∥β则 α∥β | |
| B. | 若γ丄α,γ丄β,则 α∥β | |
| C. | 若l∥m且 l?α,m?β,l∥β,m∥α,则 α∥β | |
| D. | 若l,m 异面,且 l?α,m?β,l∥β,m∥α,则 α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 患病 | 未患病 | 总计 | |
| 服用药 | 15 | 40 | 55 |
| 没服用药 | 20 | 25 | 45 |
| 总计 | 35 | 65 | 100 |
| P( K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.025 | B. | 0.05 | C. | 0.010 | D. | 0.10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com