
| A. | 若l丄α,l∥β则 α∥β | |
| B. | 若γ丄α,γ丄β,则 α∥β | |
| C. | 若l∥m且 l?α,m?β,l∥β,m∥α,则 α∥β | |
| D. | 若l,m 异面,且 l?α,m?β,l∥β,m∥α,则 α∥β |
分析 由由线面平行的性质定理和面面垂直的判定定理,即可判断A;
由面面垂直的性质和面面平行的判定,即可判断B;
由线面平行的性质定理及面面平行的判定定理,即可判断C;
由线面平行的性质定理及面面平行的判定定理,即可判断D.
解答 解:对于A,若l丄α,l∥β,由线面平行的性质定理可得l平行于过l的平面与β的交线m,可得m丄α,
由面面垂直的判定定理可得α⊥β,故A错;
对于B,若γ丄α,γ丄β,则α∥β或α,β相交,故B错;
对于C,若l∥m且 l?α,m?β,l∥β,m∥α,则α∥β或α,β相交,故C错;
对于D,若l,m 异面,且 l?α,m?β,l∥β,m∥α,
由线面平行的性质定理可得l平行于过l的平面与β的交线a,m平行于过m的平面与α的交线b,
由面面平行的判定定理可得α∥β.
故选:D.
点评 本题考查空间线面的位置关系,主要是平行与垂直的判定和性质定理的运用,考查推理能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分不必要条件 | D. | 必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
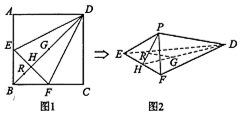 如图l,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,点G,R分别在线段DH,HB上,且$\frac{DG}{GH}$=$\frac{BR}{RH}$.将△AED,△CFD,△BEF分别沿DE,DF,EF折起,使点A,B,C重合于点P,如图2所示,
如图l,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,点G,R分别在线段DH,HB上,且$\frac{DG}{GH}$=$\frac{BR}{RH}$.将△AED,△CFD,△BEF分别沿DE,DF,EF折起,使点A,B,C重合于点P,如图2所示,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
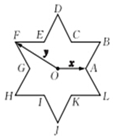 将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.
将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com