
���� ��1����ֱ��L1��x=-2��x=��cos�ȣ�y=��sin�ȣ������ֱ��L1�ļ����귽�̣�������$C��\left\{\begin{array}{l}x=2cos��\\ y=2+2sin��\end{array}\right.$����Ϊ��������Բ��C��0��2�����뾶r=2�����������C�ļ����귽�̣�
��2������$\left\{\begin{array}{l}��=4sin��\\ ��=\frac{��}{4}\end{array}\right.$����$|MN|=2\sqrt{2}$��������C�ǰ뾶Ϊr=2��Բ����CM��CN���ɴ��������CMN�������l1��l2����ļ����꣮
��� �⣺��1����ֱ��L1��x=-2��x=��cos�ȣ�y=��sin�ȣ�
��ֱ��L1�ļ����귽��Ϊ����cos��+2=0��
������$C��\left\{\begin{array}{l}x=2cos��\\ y=2+2sin��\end{array}\right.$����Ϊ��������Բ��C��0��2�����뾶r=2��
������C�ļ����귽��Ϊ��=4sin�ȣ�
��2������$\left\{\begin{array}{l}��=4sin��\\ ��=\frac{��}{4}\end{array}\right.$����$\left\{\begin{array}{l}��=0\\ ��=\frac{��}{4}\end{array}\right.$��$\left\{\begin{array}{l}��=2\sqrt{2}\\ ��=\frac{��}{4}\end{array}\right.$
��$|MN|=2\sqrt{2}$��
������C�ǰ뾶Ϊr=2��Բ��
��CM��CN��
��${S_{��CMN}}=\frac{1}{2}{r^2}=2$��
�ⷽ����$\left\{\begin{array}{l}��cos��+2=0\\ ��=\frac{��}{4}\end{array}\right.$����ֱ�߽���ļ�����Ϊ$��-2\sqrt{2}��\frac{��}{4}��$��
���� ���⿼��ֱ�ߡ����ߵļ����귽�̵��������ļ�����������е��⣬����ʱҪ�������⣬ע��������̡�ֱ�����귽�̡������귽�̻�����ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ǰ����� | B�� | Сǰ����� | C�� | ������ʽ���� | D�� | ����������ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
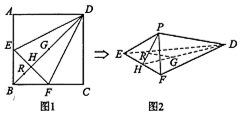 ��ͼl����������ABCD�У���E��F�ֱ���AB��BC���е㣬BD��EF���ڵ�H����G��R�ֱ����߶�DH��HB�ϣ���$\frac{DG}{GH}$=$\frac{BR}{RH}$������AED����CFD����BEF�ֱ���DE��DF��EF����ʹ��A��B��C�غ��ڵ�P����ͼ2��ʾ��
��ͼl����������ABCD�У���E��F�ֱ���AB��BC���е㣬BD��EF���ڵ�H����G��R�ֱ����߶�DH��HB�ϣ���$\frac{DG}{GH}$=$\frac{BR}{RH}$������AED����CFD����BEF�ֱ���DE��DF��EF����ʹ��A��B��C�غ��ڵ�P����ͼ2��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
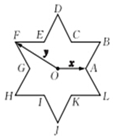 ��Բ�������ȷֵ�ֳ���ͬ�����飬����ÿ�������㹹�ɵ������������γ�ȥ�ڲ��������߶κ�����γ�һ���������ǣ���ͼ��ʾ���������ǵ�����Ϊ��O������x��y�ֱ�Ϊ��O�����������������������O����������12�������������д��ax+by����ʽ����a+b�����ֵΪ5��
��Բ�������ȷֵ�ֳ���ͬ�����飬����ÿ�������㹹�ɵ������������γ�ȥ�ڲ��������߶κ�����γ�һ���������ǣ���ͼ��ʾ���������ǵ�����Ϊ��O������x��y�ֱ�Ϊ��O�����������������������O����������12�������������д��ax+by����ʽ����a+b�����ֵΪ5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
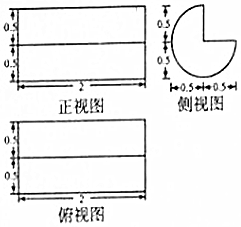 ijͬѧ���˶���������һʵ�����ӣ�������ͼ��ͼ��ʾ������ͼ��Բ��һ���ּ���Բ���������ഹֱ�İ뾶���йسߴ���ͼ����λ��m�������˽⣬����������ӵ�ƽ���ɱ�Ϊ240Ԫ/m3����ô�����ӵĽ���ɱ�ԼΪ���С�3.14����������
ijͬѧ���˶���������һʵ�����ӣ�������ͼ��ͼ��ʾ������ͼ��Բ��һ���ּ���Բ���������ഹֱ�İ뾶���йسߴ���ͼ����λ��m�������˽⣬����������ӵ�ƽ���ɱ�Ϊ240Ԫ/m3����ô�����ӵĽ���ɱ�ԼΪ���С�3.14����������| A�� | 94.20Ԫ | B�� | 240.00Ԫ | C�� | 282.60Ԫ | D�� | 376.80Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com