
分析 利用倍角公式、诱导公式化简f(x),利用其单调性可得f(x)的值域,再利用绝对值不等式的解法即可得出.
解答 解:函数$f(x)=4sinx•{sin^2}({\frac{π}{4}+\frac{x}{2}})+cos2x$
=4sinx•$\frac{1-cos(\frac{π}{2}+x)}{2}$+cos2x=2sinx(1+sinx)+1-2sin2x=2sinx+1,
∵$\frac{π}{6}≤x≤\frac{2π}{3}$,∴sinx∈$[\frac{1}{2},1]$,∴f(x)∈[2,3].
∵|f(x)-m|<2成立的充分条件是$\frac{π}{6}≤x≤\frac{2π}{3}$,
∴f(x)-2<m<f(x)+2,即0<m<5.
则实数m的取值范围为(0,5).
故答案为:(0,5).
点评 本题考查了倍角公式、诱导公式、三角函数的单调性、绝对值不等式的解法、充要条件,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{43}{48}$ | B. | $-\frac{11}{24}$ | C. | $\frac{29}{36}$ | D. | $\frac{11}{48}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
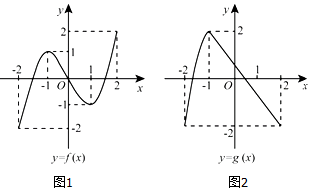
| A. | 函数f[g(x)]的零点有且仅有6个 | B. | 函数g[f(x)]的零点有且仅有3个 | ||
| C. | 函数f[f(x)]的零点有且仅有5个 | D. | 函数g[g(x)]的零点有且仅有4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com