
【题目】已知点![]() ,圆
,圆![]() .
.
(1)若直线![]() 过点
过点![]() 且到圆心
且到圆心![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 的斜率为负),当
的斜率为负),当![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)对直线![]() 的斜率是否存在进行分类讨论,利用圆心到直线
的斜率是否存在进行分类讨论,利用圆心到直线![]() 的距离等于2可求得直线
的距离等于2可求得直线![]() 的方程;
的方程;
(2)先通过点到直线的距离及勾股定理可解得直线![]() 的斜率,然后将直线
的斜率,然后将直线![]() 的方程与圆的方程联立,求出线段
的方程与圆的方程联立,求出线段![]() 的中点,作为圆心,并求出所求圆的半径,进而可得出所求圆的方程.
的中点,作为圆心,并求出所求圆的半径,进而可得出所求圆的方程.
(1)由题意知,圆![]() 的标准方程为
的标准方程为![]() ,
,![]() 圆心
圆心![]() ,半径
,半径![]() ,
,
①当直线![]() 的斜率
的斜率![]() 存在时,设直线的方程为
存在时,设直线的方程为![]() ,即
,即![]() ,
,
则圆心到直线![]() 的距离为
的距离为![]() ,
,![]() .
.
![]() 直线
直线![]() 的方程为
的方程为![]() ;
;
②当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
此时圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,符合题意.
,符合题意.
综上所述,直线![]() 的方程为
的方程为![]() 或
或![]() ;
;
(2)依题意可设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
则圆心![]() 到直线
到直线![]() 的距离
的距离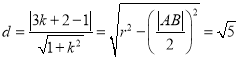 ,
,
![]() ,解得
,解得![]() 或
或![]() ,
,
又![]() ,
,![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() 即
即![]() ,
,
设点![]() 、
、![]() ,联立直线
,联立直线![]() 与圆
与圆![]() 的方程得
的方程得 ,
,
消去![]() 得
得![]() ,
,![]() ,
,
则线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,把
,把![]() 代入直线
代入直线![]() 中得
中得![]() ,
,
所以,线段![]() 的中点的坐标为
的中点的坐标为![]() ,
,
由题意知,所求圆的半径为:![]() ,
,
![]() 以线段
以线段![]() 为直径的圆的方程为:
为直径的圆的方程为:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点B是
的直径,点B是![]() 上与A,C不重合的动点,
上与A,C不重合的动点,![]() 平面
平面![]() .
.

(1)当点B在什么位置时,平面![]() 平面
平面![]() ,并证明之;
,并证明之;
(2)请判断,当点B在![]() 上运动时,会不会使得
上运动时,会不会使得![]() ,若存在这样的点B,请确定点B的位置,若不存在,请说明理由.
,若存在这样的点B,请确定点B的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,D是边AC上一点,将
,D是边AC上一点,将![]() 沿BD折起,得到三棱锥
沿BD折起,得到三棱锥![]() .若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设
.若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设![]() ,则x的取值范围为()
,则x的取值范围为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地海军航空实验班面向全省遴选学员,有![]() 名初中毕业生踊跃报名投身国防,经过文化考试、体格测试、政治考核、心理选拔等过程筛选,最终招收
名初中毕业生踊跃报名投身国防,经过文化考试、体格测试、政治考核、心理选拔等过程筛选,最终招收![]() 名学员。培养学校在关注学员的文化素养同时注重学员的身体素质,要求每月至少参加一次野营拉练活动(下面简称“活动”)并记录成绩.
名学员。培养学校在关注学员的文化素养同时注重学员的身体素质,要求每月至少参加一次野营拉练活动(下面简称“活动”)并记录成绩.![]() 月某次活动中海航班学员成绩统计如图所示:
月某次活动中海航班学员成绩统计如图所示:

(1)根据图表,试估算学员在活动中取得成绩的中位数(精确到![]() );
);
(2)根据成绩从![]() 、
、![]() 两组学员中任意选出两人为一组,若选出成绩分差大于
两组学员中任意选出两人为一组,若选出成绩分差大于![]() ,则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率.
,则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() ,
,![]() 轴被曲线
轴被曲线![]() 截得的线段长等于C1的长半轴长.
截得的线段长等于C1的长半轴长.
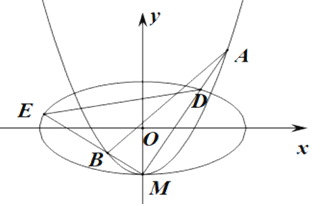
(1)求实数b的值;
(2)设C2与![]() 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线![]() 与C2相交于点A、B,直线MA、MB分别与C1交于点D、E.
与C2相交于点A、B,直线MA、MB分别与C1交于点D、E.
①证明:![]() ;
;
②记△MAB,△MDE的面积分别是![]() 若
若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】男运动员6名,女运动员4名,其中男女队长各1名.选派5人外出比赛,在下列情形中各有多少种选派方法?
(1)男运动员3名,女运动员2名;
(2)至少有1名女运动员;
(3)队长中至少有1人参加;
(4)既要有队长,又要有女运动员.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内的两点![]() 满足条件:①
满足条件:①![]() 都在函数
都在函数![]() 的图象上;②
的图象上;②![]() 关于原点对称.则称点对
关于原点对称.则称点对![]() 是函数
是函数![]() 的一对“友好点对”(点对
的一对“友好点对”(点对![]() 与
与![]() 看作同一对“友好点对”).已知函数
看作同一对“友好点对”).已知函数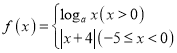 (
(![]() 且
且![]() ),若此函数的“友好点对”有且只有一对,则
),若此函数的“友好点对”有且只有一对,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com