
【题目】如图,某地有三家工厂,分别位于矩形ABCD 的顶点A、B 及CD的中点P 处,已知AB=20km,CB =10km ,为了处理三家工厂的污水,现要在矩形ABCD 的区域上(含边界),且与A、B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP ,设排污管道的总长度为![]() km.
km.
(1)按下列要求写出函数关系式:①设∠BAO= ![]() (rad),将
(rad),将![]() 表示成
表示成![]() 的函数;②设OP
的函数;②设OP ![]() (km) ,将
(km) ,将![]() 表示成
表示成![]() 的函数.
的函数.
(2)请选用(1)中的一个函数关系式,确定污水处理厂的位置,使铺设的排污管道总长度最短.

【答案】(1)①![]()
![]() ②
②![]() (2)当污水处理厂建在矩形区域内且到A、B的距离均为
(2)当污水处理厂建在矩形区域内且到A、B的距离均为![]() (km)时,铺设的排污管道总长度最短.
(km)时,铺设的排污管道总长度最短.
【解析】试题分析:(1)第(1)问第①问,先根据已知把![]() 表示成
表示成![]() 的函数,再利用三角恒等变换的知识化简函数. 第②问,直接利用两点间的距离公式把
的函数,再利用三角恒等变换的知识化简函数. 第②问,直接利用两点间的距离公式把![]() 表示成
表示成![]() 的函数.(2)第(2)问,先对函数求导,再求出函数的单调区间,最后根据单调区间得到函数的最小值.
的函数.(2)第(2)问,先对函数求导,再求出函数的单调区间,最后根据单调区间得到函数的最小值.
试题解析:
(1)①由条件知PQ 垂直平分AB,若∠BAO= ![]() (rad) ,
(rad) ,
则![]() , 故
, 故![]() ,又OP=
,又OP=![]() ,
,
所以![]() ,
,
所求函数关系式为![]()
![]()
②若OP= ![]() (km) ,则OQ=10-
(km) ,则OQ=10-![]() ,
,
所以OA =OB=![]()
所求函数关系式为![]()
(2)选择函数模型①,![]()
令![]() 0 得sin
0 得sin ![]() ,因为
,因为![]() ,所以
,所以![]() =
=![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 是
是![]() 的减函数;当
的减函数;当![]() 时,
时, ![]() ,
, ![]() 是
是![]() 的增函
的增函
数,所以函数![]() 在
在![]() =
=![]() 时取得极小值,这个极小值就是最小值.
时取得极小值,这个极小值就是最小值. ![]() .这时
.这时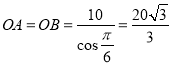 (km)
(km)
因此,当污水处理厂建在矩形区域内且到A、B的距离均为![]() (km)时,铺设的排污管道总长度最短.
(km)时,铺设的排污管道总长度最短.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 是单调递增函数,求实数
是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有两个实数根
内有两个实数根![]() ,记
,记![]() ,求实数
,求实数![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=![]() AD,E,F分别为PC,BD的中点.
AD,E,F分别为PC,BD的中点.

求证:(1)EF∥平面PAD;
(2)PA⊥平面PDC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() =1(a>0,b>0)上一点C,过双曲线中心的直线交双曲线于A,B两点,记直线AC,BC的斜率分别为k1 , k2 , 当
=1(a>0,b>0)上一点C,过双曲线中心的直线交双曲线于A,B两点,记直线AC,BC的斜率分别为k1 , k2 , 当 ![]() +ln|k1|+ln|k2|最小时,双曲线离心率为( )
+ln|k1|+ln|k2|最小时,双曲线离心率为( )
A.![]()
B.![]()
C.![]() +1
+1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1= ![]() ,an+1=
,an+1= ![]() (n∈N*).
(n∈N*).
(1)求a2 , a3的值;
(2)证明:不等式0<an<an+1对于任意n∈N*都成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,⊙O1与⊙O2外切于点P,从⊙O1上点A作的切线AB,切点为B,连AP(不过O1)并延长与⊙O2交于点C. 
(1)求证:AO1∥CO2;
(2)若 ![]() ,求⊙O1的半径与⊙O2的半径之比.
,求⊙O1的半径与⊙O2的半径之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 
(1)证明:PB∥平面AEC;
(2)设二面角D﹣AE﹣C为60°,AP=1,AD= ![]() ,求三棱锥E﹣ACD的体积.
,求三棱锥E﹣ACD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M,N分别是PA,BC的中点,且AD=2PD=2.

(1)求证:MN∥平面PCD;
(2)求证:平面PAC⊥平面PBD;
(3)求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2x-2sin2x-a.
①若f(x)=0在x∈R上有解,则a的取值范围是______;
②若x1,x2是函数y=f(x)在[0,![]() ]内的两个零点,则sin(x1+x2)=______
]内的两个零点,则sin(x1+x2)=______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com