
【题目】已知函数f(x)=2sin2x-2sin2x-a.
①若f(x)=0在x∈R上有解,则a的取值范围是______;
②若x1,x2是函数y=f(x)在[0,![]() ]内的两个零点,则sin(x1+x2)=______
]内的两个零点,则sin(x1+x2)=______
【答案】[![]() ,
,![]() ]
] ![]()
【解析】
①利用三角函数的公式化简,f(x)=0在x∈R上有解,转化为两个函数图象有交点问题即可求解;
②x1,x2是函数y=f(x)在[0,![]() ]内的两个零点,即么x1,x2是关于在[0,
]内的两个零点,即么x1,x2是关于在[0,![]() ]内的对称轴是对称的.即可求解
]内的对称轴是对称的.即可求解
f(x)=2sin2x﹣2sin2x﹣a=2sin2x﹣(1﹣cos2x)﹣a
=2sin2x+cos2x﹣1﹣a![]() 1﹣a.其中tanθ
1﹣a.其中tanθ![]()
①f(x)=0在x∈R上有解,则![]() sin(2x+θ)=a+1有解,
sin(2x+θ)=a+1有解,
∵![]()
∴![]() a+1
a+1![]() .
.
则a的取值范围是[![]() ,
,![]() ],
],
故答案为:[![]() ,
,![]() ]
]
②∵x1,x2是函数y=f(x)在[0,![]() ]内的两个零点,
]内的两个零点,
那么x1,x2是关于在[0,![]() ]内的对称轴是对称的.
]内的对称轴是对称的.
由f(x)![]() 1﹣a.其中tanθ
1﹣a.其中tanθ![]()
其对称轴2x+θ![]() kπ,k∈Z.
kπ,k∈Z.
x1,x2是关于在![]() ]内的对称轴是对称的.
]内的对称轴是对称的.
又![]() [0,
[0,![]() ],且tanθ
],且tanθ![]()
∴对称轴x![]()
∴x1+x2![]() .
.
则sin(x1+x2)=sin(![]() )=cosθ.
)=cosθ.
∵tanθ![]() ,即
,即![]() ,
,
∴cosθ![]() ,
,
则sin(x1+x2)![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,某地有三家工厂,分别位于矩形ABCD 的顶点A、B 及CD的中点P 处,已知AB=20km,CB =10km ,为了处理三家工厂的污水,现要在矩形ABCD 的区域上(含边界),且与A、B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP ,设排污管道的总长度为![]() km.
km.
(1)按下列要求写出函数关系式:①设∠BAO= ![]() (rad),将
(rad),将![]() 表示成
表示成![]() 的函数;②设OP
的函数;②设OP ![]() (km) ,将
(km) ,将![]() 表示成
表示成![]() 的函数.
的函数.
(2)请选用(1)中的一个函数关系式,确定污水处理厂的位置,使铺设的排污管道总长度最短.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45,点E、F分别为棱AB、PD的中点.

(1)求证:AF∥平面PCE;
(2)求三棱锥C-BEP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C, AB=3,BC=5.

(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)求点C到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P﹣ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.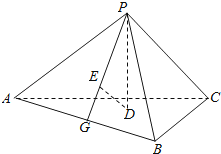
(1)证明:G是AB的中点;
(2)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.
(1)求 ![]() ;
;
(2)除H以外,直线MH与C是否有其它公共点?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|x+1|﹣|2x﹣3|.
(1)在图中画出y=f(x)的图象;
(2)求不等式|f(x)|>1的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a-![]() -lnx,g(x)=ex-ex+1.
-lnx,g(x)=ex-ex+1.
(1)若a=2,求函数f(x)在点(1,f(1))处的切线方程;
(2)若f(x)=0恰有一个解,求a的值;
(3)若g(x)≥f(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)=a-![]() (a∈R,e为自然对数的底数).
(a∈R,e为自然对数的底数).
(1)判定并证明f(x)的单调性;
(2)若对任意实数x,f(x)>m2-4m+2恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com