
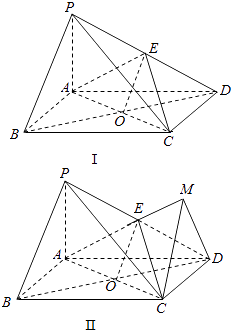
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 
(1)证明:PB∥平面AEC;
(2)设二面角D﹣AE﹣C为60°,AP=1,AD= ![]() ,求三棱锥E﹣ACD的体积.
,求三棱锥E﹣ACD的体积.
【答案】
(1)证明:连接BD交AC于O点,连接EO,
∵O为BD中点,E为PD中点,
∴EO∥PB,(2分)
EO平面AEC,PB平面AEC,所以PB∥平面AEC;(6分)
(2)解:延长AE至M连结DM,使得AM⊥DM,
∵四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,
∴CD⊥平面AMD,
∵二面角D﹣AE﹣C为60°,
∴∠CMD=60°,
∵AP=1,AD= ![]() ,∠ADP=30°,
,∠ADP=30°,
∴PD=2,
E为PD的中点.AE=1,
∴DM= ![]() ,
,
CD= ![]() =
= ![]() .
.
三棱锥E﹣ACD的体积为: ![]() =
= ![]() =
= ![]() .
.
【解析】(1)连接BD交AC于O点,连接EO,只要证明EO∥PB,即可证明PB∥平面AEC;(2)延长AE至M连结DM,使得AM⊥DM,说明∠CMD=60°,是二面角的平面角,求出CD,即可三棱锥E﹣ACD的体积.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2x﹣sin2xsinφ﹣2cos2xsin2 ![]() (0<φ<
(0<φ< ![]() )的图象的一个对称中心为(
)的图象的一个对称中心为( ![]() ,0),则下列说法不正确的是( )
,0),则下列说法不正确的是( )
A.直线x= ![]() π是函数f(x)的图象的一条对称轴
π是函数f(x)的图象的一条对称轴
B.函数f(x)在[0, ![]() ]上单调递减
]上单调递减
C.函数f(x)的图象向右平移 ![]() 个单位可得到y=cos2x的图象
个单位可得到y=cos2x的图象
D.函数f(x)在x∈[0, ![]() ]上的最小值为﹣1
]上的最小值为﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地有三家工厂,分别位于矩形ABCD 的顶点A、B 及CD的中点P 处,已知AB=20km,CB =10km ,为了处理三家工厂的污水,现要在矩形ABCD 的区域上(含边界),且与A、B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP ,设排污管道的总长度为![]() km.
km.
(1)按下列要求写出函数关系式:①设∠BAO= ![]() (rad),将
(rad),将![]() 表示成
表示成![]() 的函数;②设OP
的函数;②设OP ![]() (km) ,将
(km) ,将![]() 表示成
表示成![]() 的函数.
的函数.
(2)请选用(1)中的一个函数关系式,确定污水处理厂的位置,使铺设的排污管道总长度最短.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为原点,以x轴正半轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρsinθ+3=0,直线l的参数方程为  ,(t为参数).
,(t为参数).
(1)写出曲线C和直线l的直角坐标方程;
(2)若点A,B是曲线C上的两动点,点P是直线l上一动点,求∠APB的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品在近![]() 天内每件的销售价格
天内每件的销售价格![]() (元)与时间
(元)与时间![]() (天)的函数关系是:
(天)的函数关系是:
![]() ,该商品的日销售量
,该商品的日销售量![]() (件)与时间
(件)与时间![]() (天)的函数关系是
(天)的函数关系是![]() ,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是
,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是![]() 天中的第几天?(商品的日销售金额=该商品的销售价格
天中的第几天?(商品的日销售金额=该商品的销售价格![]() 日销售量)
日销售量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点列{An}、{Bn}分别在某锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+1 , n∈N* , |BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+1 , n∈N* , (P≠Q表示点P与Q不重合)若dn=|AnBn|,Sn为△AnBnBn+1的面积,则( )
A.{Sn}是等差数列
B.{Sn2}是等差数列
C.{dn}是等差数列
D.{dn2}是等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45,点E、F分别为棱AB、PD的中点.

(1)求证:AF∥平面PCE;
(2)求三棱锥C-BEP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|x+1|﹣|2x﹣3|.
(1)在图中画出y=f(x)的图象;
(2)求不等式|f(x)|>1的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com