
【题目】如图,已知四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
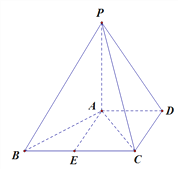
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)求点D到平面![]() 的距离.
的距离.
【答案】(1) 异面直线![]() 与
与![]() 所成角为
所成角为![]() ;(2)1.
;(2)1.
【解析】试题分析:(1)因为![]() 平面
平面![]() ,取
,取![]() 的中点
的中点![]() ,则
,则![]() 两两垂直,以
两两垂直,以![]() 点为原点以
点为原点以![]() 为轴,建立空间直角坐标系
为轴,建立空间直角坐标系![]() ,分别求出异面直线
,分别求出异面直线![]() 与
与![]() 的方向向量,利用空间向量夹角余弦公式求解即可;(2)先求得
的方向向量,利用空间向量夹角余弦公式求解即可;(2)先求得![]() ,又∵
,又∵![]() 平面
平面![]() ,
, ![]() 是平面
是平面![]() 的一个法向量,所以点
的一个法向量,所以点![]() 到平面
到平面![]() 的距离
的距离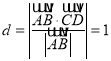 .
.
试题解析:(1)如图所示,以![]() 点为原点建立空间直角坐标系
点为原点建立空间直角坐标系![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,故
,故![]() ,
, ![]() ,
, ![]()
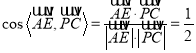 ,即
,即![]() ,
,
故异面直线![]() 与
与![]() 所成角为
所成角为![]() ;
;
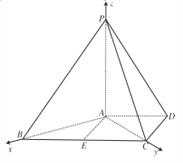
(2)在平面![]() 中,∵
中,∵![]() ,
, ![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,由
,由![]() 得
得![]() ,
,
∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,又∵
,又∵![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的一个法向量,所以点D到平面
的一个法向量,所以点D到平面![]() 的距离
的距离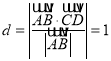
【方法点晴】本题主要考查利用空间向量求线面角,以及利用向量求点面距离,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-P2-x,则下列结论正确的是( )
A. ![]() ,
,![]() 为奇函数且为R上的减函数
为奇函数且为R上的减函数
B. ![]() ,
,![]() 为偶函数且为R上的减函数
为偶函数且为R上的减函数
C. ![]() ,
,![]() 为奇函数且为R上的增函数
为奇函数且为R上的增函数
D. ![]() ,
,![]() 为偶函数且为R上的增函数
为偶函数且为R上的增函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若任意的a、b∈[-1,1],当a+b≠0时,总有![]() .
.
(1)判断函数f(x)在[-1,1]上的单调性,并证明你的结论;
(2)解不等式:![]() ;
;
(3)若f(x)≤m2-2pm+1对所有的x∈[-1,1]恒成立,其中p∈[-1,1](p是常数),试用常数p表示实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 是单调递增函数,求实数
是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有两个实数根
内有两个实数根![]() ,记
,记![]() ,求实数
,求实数![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家通过研究学生的学习行为发现;学生的接受能力与老师引入概念和描述问题所用的时间相关,教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用![]() 表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系: ![]()

(1)开讲后第5min与开讲后第20min比较,学生的接受能力何时更强一些?
(2)开讲后多少min学生的接受能力最强?能维持多少时间?
(3)若一个新数学概念需要55以上(包括55)的接受能力以及13min时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,满足c=1,且cosBsinC+(a﹣sinB)cos(A+B)=0
(1)求C的大小;
(2)求a2+b2的最大值,并求取得最大值时角A,B的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=![]() AD,E,F分别为PC,BD的中点.
AD,E,F分别为PC,BD的中点.

求证:(1)EF∥平面PAD;
(2)PA⊥平面PDC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 
(1)证明:PB∥平面AEC;
(2)设二面角D﹣AE﹣C为60°,AP=1,AD= ![]() ,求三棱锥E﹣ACD的体积.
,求三棱锥E﹣ACD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com