
分析 由题意可得直线BM的方程,且点A关于直线BM的对称点A′(x,y)在直线BC上,求出A′的坐标即可求出直线BC的方程.
解答 解:直线BM的方程为$\frac{y-0}{2-0}$=$\frac{x-5}{4-5}$,
化为一般方程是2x+y-10=0;
设A关于直线BM的对称点为A′(x,y),
则2•$\frac{x+8}{2}$+$\frac{y-1}{2}$-10=0①,且$\frac{y+1}{x-8}$•(-2)=-1②;
由①②组成方程组,解得x=4,y=-3,即A′(4,-3);
由对称性知A′在BC边所在的直线上,
所以直线BC的斜率k不存在;
故直线BC的方程为:x=4.
点评 本题考查了求直线方程的应用问题,也考查了点关于直线的对称问题,是基础题目.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:解答题
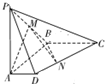 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB的中点.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
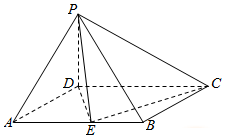 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=PD=1,AB=2,ABCD为矩形,点E是线段AB中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=PD=1,AB=2,ABCD为矩形,点E是线段AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是真命题且q是假命题 | B. | p是真命题且q是真命题 | ||
| C. | p是假命题且q是真命题 | D. | p是假命题且q是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | $\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com