
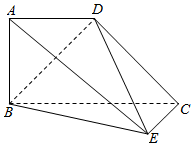
 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥底面BEC,EC⊥CB,已知BC=2,AD=AB=EC=1.
如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥底面BEC,EC⊥CB,已知BC=2,AD=AB=EC=1.分析 (I)以C为原点建立空间直角坐标系,求出$\overrightarrow{BD}$,$\overrightarrow{CE}$,$\overrightarrow{CD}$的坐标,利用向量的数量积为零证明BD⊥CE,BD⊥CD,故而得出BD⊥平面CDE;
(II)由(I)知$\overrightarrow{BD}$为平面CDE的一个法向量,则AE与平面CDE所成角的正弦值等于|cos<$\overrightarrow{BD}$,$\overrightarrow{AE}$>|.
解答 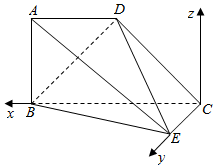 (Ⅰ)证明:过C作AB的平行线CZ,则CZ⊥平面BCE,
(Ⅰ)证明:过C作AB的平行线CZ,则CZ⊥平面BCE,
∵BC⊥EC,CB,CE,CZ两两垂直,
以C为坐标原点建立空间直角坐标系C-xyz,如图所示:
∵BC=2,AD=AB=EC=1.
∴B(2,0,0),C(0,0,0),D(1,0,1),E(0,1,0).
∴$\overrightarrow{BD}$=(-1,0,1),$\overrightarrow{CD}$=(1,0,1),$\overrightarrow{CE}$=(0,1,0).
∴$\overrightarrow{BD}•\overrightarrow{CD}$=0,$\overrightarrow{BD}$$•\overrightarrow{CE}$=0.
∴BD⊥CD,BD⊥CE,又CD?平面CDE,CE?平面CDE,CD∩CE=C,
∴BD⊥面DEC.
(Ⅱ)∵BD⊥平面CDE,∴$\overrightarrow{BD}$为平面CDE的一个法向量.
∵A(2,0,1),∴$\overrightarrow{AE}$=(-2,1,-1),
∴$\overrightarrow{AE}•\overrightarrow{BD}$=1,|$\overrightarrow{AE}$|=$\sqrt{6}$,|$\overrightarrow{BD}$|=$\sqrt{2}$,
∴cos<$\overrightarrow{AE},\overrightarrow{BD}$>=$\frac{\overrightarrow{AE}•\overrightarrow{BD}}{|\overrightarrow{AE}||\overrightarrow{BD}|}$=$\frac{1}{\sqrt{6}×\sqrt{2}}$=$\frac{\sqrt{3}}{6}$.
∴AE与平面CDE所成角的正弦值为$\frac{\sqrt{3}}{6}$.
点评 本题考查了线面垂直的判定,线面角的计算,多采用向量法来解决问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
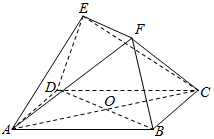 如图,多面体ABCDEF中,四边形ABCD是边长为2的正方形,四边形EFBD为等腰梯形,EF∥BD,EF=$\frac{1}{2}$BD,平面EFBD⊥平面ABCD.
如图,多面体ABCDEF中,四边形ABCD是边长为2的正方形,四边形EFBD为等腰梯形,EF∥BD,EF=$\frac{1}{2}$BD,平面EFBD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
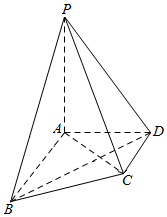 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,PA=AB=2CD=4,$PB=2AD=4\sqrt{2}$,平面PAB⊥平面ABCD.
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,PA=AB=2CD=4,$PB=2AD=4\sqrt{2}$,平面PAB⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
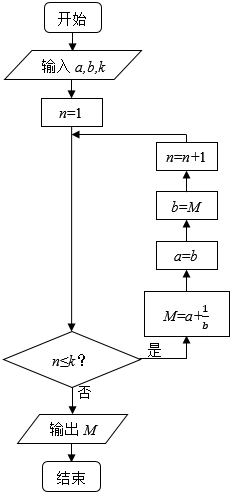 执行如图的程序框图,若输入a,b,k分别为1,2,3,则输出的M=( )
执行如图的程序框图,若输入a,b,k分别为1,2,3,则输出的M=( )| A. | $\frac{2}{3}$ | B. | $\frac{16}{5}$ | C. | $\frac{7}{2}$ | D. | $\frac{15}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
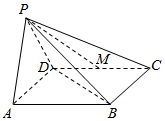 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 温差 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com