
分析 设棱锥的高为SO,则由正三角形中心的性质可得AC⊥OB,AC⊥SO,于是AC⊥平面SBO,得SB⊥AC,结合SB⊥AM可证SB⊥平面SAC,同理得出SA,SB,SC两两垂直,从而求得侧棱长,计算出体积.外接球的球心N在直线SO上,设SN=BN=r,则ON=|SO-r|,利用勾股定理列方程解出r.
解答 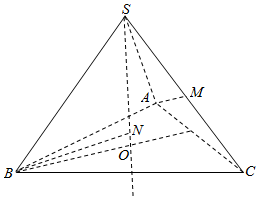 解:设O为S在底面ABC的投影,则O为等边三角形ABC的中心,
解:设O为S在底面ABC的投影,则O为等边三角形ABC的中心,
∵SO⊥平面ABC,AC?平面ABC,
∴AC⊥SO,又BO⊥AC,
∴AC⊥平面SBO,∵SB?平面SBO,
∴SB⊥AC,又AM⊥SB,AM?平面SAC,AC?平面SAC,AM∩AC=A,
∴SB⊥平面SAC,
同理可证SC⊥平面SAB.
∴SA,SB,SC两两垂直.
∵△SOA≌△SOB≌△SOC,
∴SA=SB=SC,
∵AB=2$\sqrt{2}$,∴SA=SB=SC=2.
∴三棱锥的体积V=$\frac{1}{3}{S}_{△SAC}•SB$=$\frac{1}{3}×\frac{1}{2}×2×2×2=\frac{4}{3}$.
设外接球球心为N,则N在SO上.
∵BO=$\frac{2}{3}×\frac{\sqrt{3}}{2}AB$=$\frac{2\sqrt{6}}{3}$.∴SO=$\sqrt{S{B}^{2}-B{O}^{2}}$=$\frac{2\sqrt{3}}{3}$,
设外接球半径为r,则NO=SO-r=$\frac{2\sqrt{3}}{3}$-r,NB=r,
∵OB2+ON2=NB2,∴$\frac{8}{3}$+($\frac{2\sqrt{3}}{3}-r$)2=r2,解得r=$\sqrt{3}$.
∴外接球的表面积S=4π×3=12π.
故答案为:$\frac{4}{3}$,12π.
点评 本题考查了正棱锥的结构特征,棱锥与外接球的关系,属于中档题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.| $\overrightarrow x$ | $\overrightarrow y$ | $\overrightarrow w$ | $\sum_{i=1}^8{\;}$(x1-$\overrightarrow x$)2 | $\sum_{i=1}^8{\;}$(w1-$\overrightarrow w$)2 | $\sum_{i=1}^8{\;}$(x1-$\overrightarrow x$)(y-$\overrightarrow y$) | $\sum_{i=1}^8{\;}$(w1-$\overrightarrow w$)(y-$\overrightarrow y$) |
| 46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
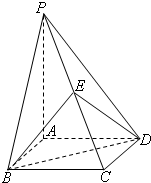 如图,四边形ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,
如图,四边形ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 使用年限x | 1 | 2 | 3 | 4 | 5 |
| 维修费用y | 1.3 | 2.5 | 4.0 | 5.6 | 6.6 |
| A. | 12.86 | B. | 13.38 | C. | 13.59 | D. | 15.02 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
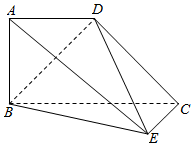 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥底面BEC,EC⊥CB,已知BC=2,AD=AB=EC=1.
如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥底面BEC,EC⊥CB,已知BC=2,AD=AB=EC=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com