
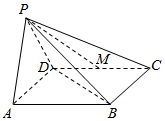
 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.分析 (1)取AD的中点E,连结PE,EM,AC.则AC∥EM,由菱形性质得BD⊥EM,又BD⊥PM,故而BD⊥平面PEM,于是BD⊥PE,又PE⊥AD,故而PE⊥平面ABCD,从而得出结论;
(2)以E为原点建立空间直角坐标系,求出平面PBM的法向量和$\overrightarrow{AB}$的坐标,计算出|cos<$\overrightarrow{n},\overrightarrow{AB}$>|即为答案.
解答 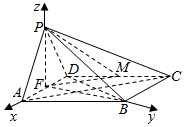 证明:(1)取AD的中点E,连结PE,EM,AC
证明:(1)取AD的中点E,连结PE,EM,AC
∵PA=PD,∴PE⊥AD.
∵底面ABCD是菱形,∴BD⊥AC,
∵E,M是AD,CD的中点,∴EM∥AC,
∴BD⊥EM,又BD⊥PM,EM?平面PEM,PM?平面PEM,EM∩PM=M,
∴BD⊥平面PEM,∵PE?平面PEM,
∴BD⊥PE,
又AD?平面ABCD,BD?平面ABCD,AD∩BD=D,
∴PE⊥平面ABCD,又PE?平面PAD,
∴平面PAD⊥平面ABCD.
(2)∵底面ABCD为菱形,且∠DAB=60°,∴△ABE是等边三角形,
∵∠APD=60°,AP=PD,∴△PAD是等边三角形.
连结BE,则BE⊥AE,
以E为坐标原点,EA,EB,EP所在直线为坐标轴建立如图所示的空间直角坐标系,
设PA=PD=2,则A(1,0,0),P(0,0,$\sqrt{3}$),M(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$,0),B(0,$\sqrt{3}$,0).
∴$\overrightarrow{AB}$=(-1,$\sqrt{3}$,0),$\overrightarrow{PB}$=(0,$\sqrt{3}$,-$\sqrt{3}$),$\overrightarrow{PM}$=(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$,-$\sqrt{3}$).
设平面PBM的法向量为$\overrightarrow{n}$=(x,y,z),则$\overrightarrow{n}•\overrightarrow{PB}=0$,$\overrightarrow{n}•\overrightarrow{PM}$=0,
∴$\left\{\begin{array}{l}{\sqrt{3}y-\sqrt{3}z=0}\\{-\frac{3}{2}x+\frac{\sqrt{3}}{2}y-\sqrt{3}z=0}\end{array}\right.$,令z=$\sqrt{3}$得$\overrightarrow{n}$=(-1,$\sqrt{3}$,$\sqrt{3}$).
∴$\overrightarrow{n}•\overrightarrow{AB}$=4,|$\overrightarrow{n}$|=$\sqrt{7}$,|$\overrightarrow{AB}$|=2,
∴cos<$\overrightarrow{n},\overrightarrow{AB}$>=$\frac{\overrightarrow{n}•\overrightarrow{AB}}{|\overrightarrow{n}||\overrightarrow{AB}|}$=$\frac{2\sqrt{7}}{7}$.
∴直线AB与平面PBM所成角的正弦值为$\frac{2\sqrt{7}}{7}$.
点评 本题考查了面面垂直的判定,线面角的计算,空间向量在立体几何中的应用,属于中档题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| 使用年限x | 1 | 2 | 3 | 4 | 5 |
| 维修费用y | 1.3 | 2.5 | 4.0 | 5.6 | 6.6 |
| A. | 12.86 | B. | 13.38 | C. | 13.59 | D. | 15.02 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
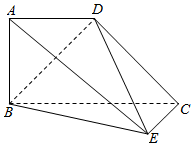 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥底面BEC,EC⊥CB,已知BC=2,AD=AB=EC=1.
如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥底面BEC,EC⊥CB,已知BC=2,AD=AB=EC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | M | 8 | 6 | 5 |
| A. | 6.4 | B. | 8 | C. | 9.6 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某茶馆为了了解热茶销售量y(杯)与气温x(℃)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
某茶馆为了了解热茶销售量y(杯)与气温x(℃)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:| 气温(℃) | 18 | 13 | 10 | -1 |
| 杯数 | 24 | 34 | 38 | 64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com