
分析 在直角坐标系里,△OAB的面积S=4-$\frac{1}{2}$(sinθ×2)-$\frac{1}{2}$[cosθ×2]-$\frac{1}{2}$(2-sinθ)(2-cosθ),利用二倍角的正弦函数公式得到一个角的正弦函数,根据正弦函数的值域及角度的范围即可得到三角形面积最大值.
解答 解:∵A(2,cosθ)、B(sinθ,2),(θ∈(0,$\frac{π}{2}$]),
∴△OAB的面积S=4-$\frac{1}{2}$(sinθ×2)-$\frac{1}{2}$[cosθ×2]-$\frac{1}{2}$(2-sinθ)(2-cosθ)=2-$\frac{1}{2}$sinθcosθ=2-$\frac{1}{4}sin2θ$,
∵2θ∈(0,π],故当2θ=π,即θ=$\frac{π}{2}$,S取最大值2.
点评 本题考查的知识点是三角形面积公式,基本利用割补法,求出三角形面积的表达式,是解答的关键.


科目:高中数学 来源: 题型:填空题
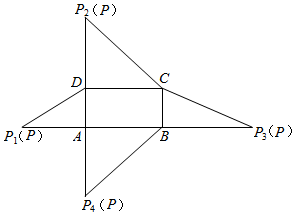
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
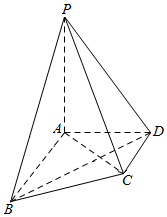 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,PA=AB=2CD=4,$PB=2AD=4\sqrt{2}$,平面PAB⊥平面ABCD.
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,PA=AB=2CD=4,$PB=2AD=4\sqrt{2}$,平面PAB⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
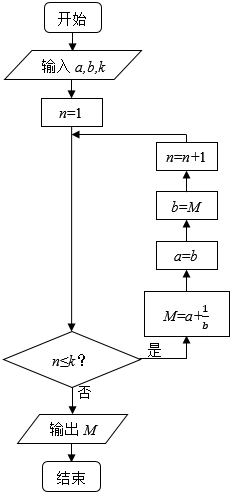 执行如图的程序框图,若输入a,b,k分别为1,2,3,则输出的M=( )
执行如图的程序框图,若输入a,b,k分别为1,2,3,则输出的M=( )| A. | $\frac{2}{3}$ | B. | $\frac{16}{5}$ | C. | $\frac{7}{2}$ | D. | $\frac{15}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
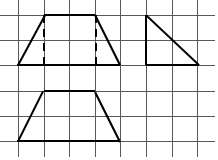
| A. | 4 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
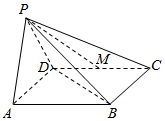 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{3},\frac{2}{3}]$ | B. | $[\frac{1}{6},\frac{4}{3}]$ | C. | $[\frac{1}{3},\frac{4}{3}]$ | D. | $[\frac{2}{3},\frac{4}{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,|AB|=4,点E为AB的中点,点D为线段AB垂直平分线上的一点,且|DE|=3,固定边AB,在平面ABD内移动顶点C,使得△ABC的内切圆始终与AB切于线段BE的中点,且C、D在直线AB的同侧,在移动过程中,当|CA|+|CD|取得最小值时,点C到直线DE的距离为$2\sqrt{15}-6$.
如图,在△ABC中,|AB|=4,点E为AB的中点,点D为线段AB垂直平分线上的一点,且|DE|=3,固定边AB,在平面ABD内移动顶点C,使得△ABC的内切圆始终与AB切于线段BE的中点,且C、D在直线AB的同侧,在移动过程中,当|CA|+|CD|取得最小值时,点C到直线DE的距离为$2\sqrt{15}-6$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com