
 某茶馆为了了解热茶销售量y(杯)与气温x(℃)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
某茶馆为了了解热茶销售量y(杯)与气温x(℃)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:| 气温(℃) | 18 | 13 | 10 | -1 |
| 杯数 | 24 | 34 | 38 | 64 |
分析 (1)作出散点图,根据散点图判断是否线性相关;
(2)根据回归系数公式计算回归系数,得出回归方程;
(3)把x=20代入回归方程计算.
解答 解:(1)作出散点图,
从散点图可以看出,销售量y(杯)与气温x(℃)有比较好的线性相关关系,
∴可以用线性回归方程刻画它们之间的关系.
(2)$\overline{x}$=$\frac{1}{4}$×(18+13+10-1)=10,$\overline{y}$=$\frac{1}{4}$×(24+34+38+64)=40.
$\sum_{i=1}^{4}{x}_{i}{y}_{i}$=18×24+13×34+10×38-1×64=1190,$\sum_{i=1}^{4}{{x}_{i}}^{2}$=182+132+102+1=594.
$\stackrel{∧}{b}$=$\frac{1190-4×10×40}{594-4×1{0}^{2}}$=-$\frac{410}{195}$≈-2.1,$\stackrel{∧}{a}$=40-(-2.1)×10=61,
∴线性回归方程为$\stackrel{∧}{y}$=-2.1x+61.
(3)当x=20时,$\stackrel{∧}{y}$=-2.1×20+61=19.
∴当气温为20℃时,热茶约能销售19杯.
点评 本题考查了线性回归方程的求解及数值预测,属于中档题.


科目:高中数学 来源: 题型:解答题
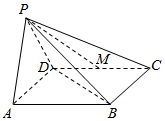 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 温差 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,|AB|=4,点E为AB的中点,点D为线段AB垂直平分线上的一点,且|DE|=3,固定边AB,在平面ABD内移动顶点C,使得△ABC的内切圆始终与AB切于线段BE的中点,且C、D在直线AB的同侧,在移动过程中,当|CA|+|CD|取得最小值时,点C到直线DE的距离为$2\sqrt{15}-6$.
如图,在△ABC中,|AB|=4,点E为AB的中点,点D为线段AB垂直平分线上的一点,且|DE|=3,固定边AB,在平面ABD内移动顶点C,使得△ABC的内切圆始终与AB切于线段BE的中点,且C、D在直线AB的同侧,在移动过程中,当|CA|+|CD|取得最小值时,点C到直线DE的距离为$2\sqrt{15}-6$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com