
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用函数的最值判断①的正误;利用三角函数的平移伸缩变换判断②的正误;利用正态分布的性质判断③的正误;利用二项式定理展开式判断④的正误.
解答 解:对于①,函数y=sin2x-$\sqrt{3}$cos2x=$2sin(2x-\frac{π}{3})$,x=$\frac{5π}{3}$时,$2sin(2×\frac{5π}{3}-\frac{π}{3})=0$,所以直线x=$\frac{5π}{3}$不是函数y=sin2x-$\sqrt{3}$cos2x的一条对称轴,所以①不正确.
对于②,将函数y=cos(x+$\frac{3π}{2}$)的图象上的每个点的横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),可得:y=cos(2x+$\frac{3π}{2}$),再向左平行移动$\frac{π}{4}$个单位长度得到:y=cos(2x+$\frac{π}{2}$+$\frac{3π}{2}$)=cos2x,不是函数y=sin(2x+$\frac{π}{4}$)的图象.所以②不正确.
对于③,设随机变量ξ-N(3,9),若P(ξ<α)=0.3,(a<3),则P(ξ<6-a)=0.7,所以③正确.
对于④,(2$\sqrt{x}$-$\frac{1}{x}$)10的二项展开式中,通项公式为:${C}_{10}^{r}({2\sqrt{x})}^{10-r}(-\frac{1}{x})^{r}$=$(-1)^{r}{C}_{10}^{r}{2}^{10-r}{x}^{\frac{10-3r}{2}}$,$\frac{10-3r}{2}=-1$,可得r=4,
故含有x-1项的二项式系数为:${C}_{10}^{4}$=210.故④正确.
故选:B.
点评 本题考查命题真假的判断与应用,考查三角函数的性质,二项式定理以及正态分布的性质的应用,考查计算能力,逻辑推理能力.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 科目 | 男 | 女 |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
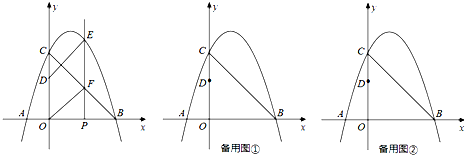
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 使用年限x | 2 | 3 | 4 | 5 |
| 维修费用y | 2 | 3.4 | 5 | 6.6 |
| A. | 7.2千元 | B. | 7.8千元 | C. | 8.1千元 | D. | 9.5千元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com