
分析 (1)利用椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的短轴长为2,F为其右焦点,P为椭圆上一点,且PF与x轴垂直,$\overrightarrow{OF}•\overrightarrow{OP}=3$及a、b、c三者关系,计算即可求椭圆C的方程;
(2)分类讨论,再设直线方程代入题意方程,利用韦达定理,及以AB弦为直径的圆过坐标原点O,即可求得结论.
解答 解:(1)由已知得2b=2,b=1,
又$\overrightarrow{OF}•\overrightarrow{OP}=|{\overrightarrow{OF}}|•|{\overrightarrow{OP}}|cos∠POF={|{\overrightarrow{OF}}|^2}={c^2}=3$,∴a2=4,
∴椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$…(5分)
(2)(i)当直线OA的斜率不存在或斜率为零时,易知$|AB|=\sqrt{{a^2}+{b^2}}=\sqrt{5}$;…(7分)
(ii)当直线OA的斜率存在且不为零时,
∵直线OA,OB互相垂直且由图象的对称性知,直线OA,OB为椭圆C有四个交点,从中任取两点作弦长AB所得的值相等.
设直线OA方程为:y=kx(k≠0)
联立:$\left\{\begin{array}{l}y=kx\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$解得:${x^2}=\frac{4}{{1+4{k^2}}}$
不妨取A$({\frac{2}{{\sqrt{1+4{k^2}}}},\frac{2k}{{\sqrt{1+4{k^2}}}}})$,同理取B$({\frac{2k}{{\sqrt{4+{k^2}}}},-\frac{2}{{\sqrt{4+{k^2}}}}})$
则|AB|=$\sqrt{{{({\frac{2}{{\sqrt{1+4{k^2}}}}-\frac{2k}{{\sqrt{4+{k^2}}}}})}^2}+{{({\frac{2k}{{\sqrt{1+4{k^2}}}}+\frac{2}{{\sqrt{4+{k^2}}}}})}^2}}$
=$2\sqrt{\frac{1}{{1+4{k^2}}}+\frac{k^2}{{4+{k^2}}}+\frac{k^2}{{1+4{k^2}}}+\frac{1}{{4+{k^2}}}}$
=$2\sqrt{\frac{{1+{k^2}}}{{1+4{k^2}}}+\frac{{{k^2}+1}}{{4+{k^2}}}}$=$2\sqrt{5\frac{{{{({{k^2}+1})}^2}}}{{({1+4{k^2}})({4+{k^2}})}}}$
=$2\sqrt{5}•\sqrt{\frac{{{k^4}+2{k^2}+1}}{{4{k^4}+17{k^2}+4}}}$<$2\sqrt{5}•\sqrt{\frac{{{k^4}+2{k^2}+1}}{{4{k^4}+8{k^2}+4}}}$=$\sqrt{5}$,
∴综上(i) (ii)可知:$|AB{|_{max}}=\sqrt{5}$…(12分)
点评 本题考查椭圆的标准方程与几何性质,考查直线与椭圆的位置关系,考查基本不等式,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于难题.


科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:选择题
如图,在直三棱柱 中,
中, ,过
,过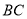 的中点
的中点 作平面
作平面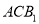 的垂线,交平面
的垂线,交平面 于
于 ,则
,则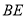 与平面
与平面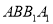 所成角的正切值为( )
所成角的正切值为( )

A.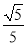 B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为a的平行线,将一根长度为l的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率p=$\frac{2l}{πa}$(π为圆周率).已知l=3.14,a=6,π≈3.14,现随机掷14根相同的针(长度为l)在这个平面上,记这些针与平行线(间距为a)相交的根数为m,其相应的概率为p(m).当p(m)取得最大值时,m=4或5.
十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为a的平行线,将一根长度为l的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率p=$\frac{2l}{πa}$(π为圆周率).已知l=3.14,a=6,π≈3.14,现随机掷14根相同的针(长度为l)在这个平面上,记这些针与平行线(间距为a)相交的根数为m,其相应的概率为p(m).当p(m)取得最大值时,m=4或5.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com