
分析 (Ⅰ)直角△ABC中,利用直角三角形中的边角关系求得AC和cosC的值,再根据AD=4DC求得CD的值,利用余弦定理求得BD的值.
(Ⅱ)在△BCD中,由正弦定理求得sin∠CDB的值.
解答 解:(Ⅰ)直角△ABC中,∵AB=4,BC=3,A=90°,∴AC=5,cosC=$\frac{3}{5}$,sinC=$\frac{4}{5}$.
∵AD=4DC,∴AD=4,CD=1,
在△BCD中,由余弦定理,BD2=BC2+CD2-2BC•CD•cosC=9+1-2×3×1×$\frac{3}{5}$=$\frac{32}{5}$,∴BD=$\frac{4\sqrt{10}}{5}$.
(Ⅱ)在△BCD中,由正弦定理,得 $\frac{CD}{sin∠CBD}$=$\frac{BD}{sinC}$,$\frac{1}{sin∠CBD}$=$\frac{\frac{4\sqrt{10}}{5}}{\frac{4}{5}}$=$\frac{3\sqrt{10}}{10}$.
点评 本题主要考查直角三角形中的边角关系,正弦定理和余弦定理的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:填空题
已知等腰梯形 的顶点都在抛物线
的顶点都在抛物线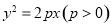 上,且
上,且 ,
, ,则点
,则点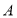 到抛物线的焦点的距离是______________.
到抛物线的焦点的距离是______________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
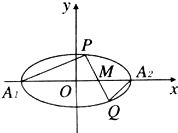
 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左、右顶点为A,B,左、右焦点为F1,F2,|AB|=4,|F1F2|=2$\sqrt{3}$.直线y=kx+m(k>0)交椭圆E于C,D两点,与线段F1F2、椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左、右顶点为A,B,左、右焦点为F1,F2,|AB|=4,|F1F2|=2$\sqrt{3}$.直线y=kx+m(k>0)交椭圆E于C,D两点,与线段F1F2、椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.
若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 科目 | 男 | 女 |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com