
分析 (1)把右焦点(c,0)代入直线可解得c.设A(x1,y1),B(x2,y2),线段AB的中点P(x0,y0),利用“点差法”即可得到a、b的关系式,再与a2=b2+c2联立即可得到a、b、c;
(2)由CD⊥AB可设直线CD的方程为y=x+t并与椭圆的方程联立得到根与系数的关系,进而可得到弦长|CD|的表达式,利用二次函数的单调性即可得到其最大值.
解答 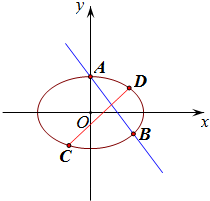 解:(1)把右焦点(c,0)代入直线x+y-$\sqrt{3}$=0,
解:(1)把右焦点(c,0)代入直线x+y-$\sqrt{3}$=0,
得c+0-$\sqrt{3}$=0,解得c=$\sqrt{3}$.
设A(x1,y1),B(x2,y2),线段AB的中点P(x0,y0),
则$\frac{{{x}_{1}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}}{{b}^{2}}$=1,$\frac{{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{2}}^{2}}{{b}^{2}}$=1,
两式相减得:$\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}-{{y}_{2}}^{2}}{{b}^{2}}$=0,
∴$\frac{{x}_{1}+{x}_{2}}{{a}^{2}}$+$\frac{{y}_{1}+{y}_{2}}{{b}^{2}}$×$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=0,
∴$\frac{2{x}_{0}}{{a}^{2}}$+$\frac{2{y}_{0}}{{b}^{2}}$×(-1)=0,
又∵kOP=$\frac{1}{2}$=$\frac{{y}_{0}}{{x}_{0}}$,∴$\frac{1}{{a}^{2}}$-$\frac{1}{2{b}^{2}}$=0,即a2=2b2.
联立得$\left\{\begin{array}{l}{{a}^{2}=2{b}^{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{c=\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}=6}\\{{b}^{2}=3}\end{array}\right.$,
∴M的方程为:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1;
(2)∵CD⊥AB,∴可设直线CD的方程为y=x+t,
联立直线CD与M的方程,消去y得:3x2+4tx+2t2-6=0,
∵直线CD与椭圆有两个不同的交点,
∴△=16t2-12(2t2-6)=72-8t2>0,解得:-3<t<3(*).
设C(x3,y3),D(x4,y4),∴x3+x4=-$\frac{4t}{3}$,x3x4=$\frac{2{t}^{2}-6}{3}$.
∴|CD|=$\sqrt{(1+{1}^{2})[({x}_{3}+{x}_{4})^{2}-4{x}_{3}{x}_{4}]}$
=$\sqrt{2[(-\frac{4t}{3})^{2}-4×\frac{2{t}^{2}-6}{3}]}$
=$\frac{2\sqrt{2}•\sqrt{18-2{t}^{2}}}{3}$.
∴当且仅当t=0时,|CD|最大值为4,满足(*).
∴|CD|最大值为4.
点评 本题综合考查了椭圆的定义、标准方程及其性质、“点差法”、中点坐标公式、直线与椭圆相交问题转化为方程联立得到一元二次方程根与系数的关系、弦长公式、二次函数的单调性等基础知识,考查了推理能力、数形结合的思想方法、计算能力、分析问题和解决问题的能力,注意解题方法的积累,属于中档题.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:解答题
 如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,求三棱锥P-AOC的体积,并求异面直线PA和OE所成角的大小.
如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,求三棱锥P-AOC的体积,并求异面直线PA和OE所成角的大小.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北邢台市高一上学期月考一数学试卷(解析版) 题型:选择题
已知函数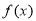 为奇函数,且当
为奇函数,且当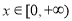 时,
时,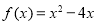 ,则
,则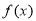 在区间
在区间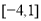 上的最大值为( )
上的最大值为( )
A.-3 B.0
C.4 D.32
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[0,\frac{1}{13}]$ | B. | $[0,\frac{5}{13}]$ | C. | $[\frac{1}{13},1]$ | D. | $[\frac{5}{13},1]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com