
分析 (1)对商品A的附加税率为p%,所以可销售80-10p万件,销售额为6400-800p万元,由此能求出p的范围.
(2)销售额为g(P)=6400-800p,2≤p≤6.利用单调递减即可求解判断.
(3)每年所获的税金k(p)=64p-8p2万元,根据二次函数性质求解即可.
解答 解:(1)对商品A的附加税率为p%,
所以可销售 80-10p 万件,销售额为6400-800p万元,
所以税额为64p-8p2万元,
64p-8p2≥96,
所以(p-2)(p-6)≤0,
所以p的范围2≤p≤6.
(2)∵销售额为g(P)=6400-800p,2≤p≤6.单调递减
∴g(P)=6400-800p,最大值为g(2)=4=6400-1600=4800万元,
此时p=2
(3)每年所获的税金k(p)=64p-8p2万元,
根据二次函数的性质得出:p=4时,金k(p)=64p-8p2取最大值.
所以k(p)取最大值时,p=4
点评 本题考查p的取值范围的求法,二次个数的单调性,最大值问题,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左、右顶点为A,B,左、右焦点为F1,F2,|AB|=4,|F1F2|=2$\sqrt{3}$.直线y=kx+m(k>0)交椭圆E于C,D两点,与线段F1F2、椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左、右顶点为A,B,左、右焦点为F1,F2,|AB|=4,|F1F2|=2$\sqrt{3}$.直线y=kx+m(k>0)交椭圆E于C,D两点,与线段F1F2、椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知棱长为2的正方体ABCD-GPHF截去一个多面体后,所得几何体如图所示,点E在GP上,且EG=1.
已知棱长为2的正方体ABCD-GPHF截去一个多面体后,所得几何体如图所示,点E在GP上,且EG=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
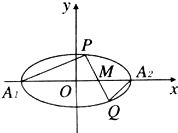 若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.
若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com