
 如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,求三棱锥P-AOC的体积,并求异面直线PA和OE所成角的大小.
如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,求三棱锥P-AOC的体积,并求异面直线PA和OE所成角的大小. 分析 由条件便知PO为三棱锥P-AOC的高,底面积S△AOC又容易得到,从而带入棱锥的体积公式即可得到该三棱锥的体积.根据条件能够得到OE∥AC,从而找到异面直线PA,OE所成角为∠PAC,可取AC中点H,连接PH,便得到PH⊥AC,从而可在Rt△PAH中求出cos∠PAC,从而得到∠PAC.
解答  解:∵PO=2,OA=1,OC⊥AB;
解:∵PO=2,OA=1,OC⊥AB;
∴${V}_{三棱锥P-AOC}=\frac{1}{3}×\frac{1}{2}×1×1×2=\frac{1}{3}$;
E为劣弧$\widehat{CB}$的中点;
∴∠BOE=45°,又∠ACO=45°;
∴OE∥AC;
∴∠PAC便是异面直线PA和OE所成角;
在△ACP中,AC=$\sqrt{2}$,$AP=CP=\sqrt{5}$;
如图,取AC中点H,连接PH,则PH⊥AC,AH=$\frac{\sqrt{2}}{2}$;
∴在Rt△PAH中,cos∠PAH=$\frac{AH}{AP}=\frac{\sqrt{10}}{10}$;
∴异面直线PA与OE所成角的大小为arccos$\frac{\sqrt{10}}{10}$.
点评 考查圆锥的定义,圆锥的高和母线,等弧所对的圆心角相等,能判断两直线平行,以及异面直线所成角的定义及找法、求法,能用反三角函数表示角.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$或$\frac{1}{16}$ | C. | $\frac{1}{16}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点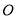 为极点,
为极点,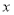 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 的极坐标为
的极坐标为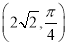 ,曲线
,曲线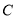 的参数方程为
的参数方程为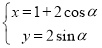 (
(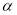 为参数).
为参数).
(1)直线 过
过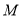 且与曲线
且与曲线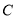 相切,求直线
相切,求直线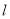 的极坐标方程;
的极坐标方程;
(2)点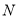 与点
与点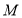 关于
关于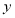 轴对称,求曲线
轴对称,求曲线 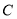 上的点到点
上的点到点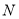 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:填空题
已知等腰梯形 的顶点都在抛物线
的顶点都在抛物线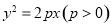 上,且
上,且 ,
, ,则点
,则点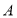 到抛物线的焦点的距离是______________.
到抛物线的焦点的距离是______________.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北邢台市高一上学期月考一数学试卷(解析版) 题型:解答题
已知函数
(1)求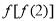 并判断函数
并判断函数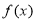 的奇偶性;
的奇偶性;
(2)若对任意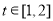 ,
,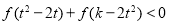 恒成立,求实数
恒成立,求实数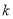 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com