
分析 (1)通过焦点坐标可设椭圆C的标准方程且a2-b2=3,将点P($\sqrt{3}$,$\frac{1}{2}$)代入椭圆方程,计算即得结论;
(2)通过△AMN是以A为直角顶点的等腰直角三角形可得直线l与x轴平行,利用kAM•kAN=-1计算即可.
解答 解:(1)∵两焦点分别为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),
∴可设椭圆C的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),a2-b2=3,①
又∵椭圆C经过点P($\sqrt{3}$,$\frac{1}{2}$),
∴$\frac{3}{{a}^{2}}+\frac{1}{4{b}^{2}}=1$,②
联立①②,解得a2=4,b2=1,
∴椭圆C的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)由(1)知,点A(0,-1)即为椭圆的下顶点,
∵△AMN是以A为直角顶点的等腰直角三角形,
∴直线l与x轴平行,设直线l方程为y=t(-1<t<1),
则M(-2$\sqrt{1-{t}^{2}}$,t),N(2$\sqrt{1-{t}^{2}}$,t),
∵kAM=-$\frac{t+1}{2\sqrt{1-{t}^{2}}}$,kAN=$\frac{t+1}{2\sqrt{1-{t}^{2}}}$,
∴kAM•kAN=-$\frac{t+1}{2\sqrt{1-{t}^{2}}}$•$\frac{t+1}{2\sqrt{1-{t}^{2}}}$=-1,
解得:t=$\frac{3}{5}$或t=-1(舍),
∴直线l方程为:y=$\frac{3}{5}$.
点评 本题考查椭圆的定义及标准方程,考查直线与椭圆的位置关系,注意解题方法的积累,属于中档题.


科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点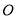 为极点,
为极点,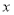 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 的极坐标为
的极坐标为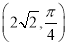 ,曲线
,曲线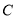 的参数方程为
的参数方程为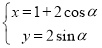 (
(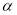 为参数).
为参数).
(1)直线 过
过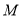 且与曲线
且与曲线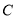 相切,求直线
相切,求直线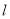 的极坐标方程;
的极坐标方程;
(2)点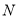 与点
与点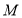 关于
关于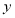 轴对称,求曲线
轴对称,求曲线 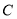 上的点到点
上的点到点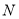 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北邢台市高一上学期月考一数学试卷(解析版) 题型:选择题
设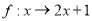 是集合
是集合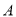 到集合
到集合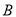 的映射,若
的映射,若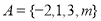 ,
,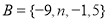 ,则
,则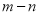 等于( )
等于( )
A.-4 B.-1
C.0 D.10
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${C}_{9}^{3}$ | B. | ${C}_{18}^{3}$ | C. | ${C}_{9}^{4}$ | D. | ${C}_{18}^{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 17 | C. | 40 | D. | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com