
【题目】春节期间爆发的新型冠状病毒(COVID-19)是新中国成立以来感染人数最多的一次疫情.一个不知道自己已感染但处于潜伏期的甲从疫区回到某市过春节,回到家乡后与朋友乙、丙、丁相聚过,最终乙、丙、丁也感染了新冠病毒.可以肯定的是乙受甲感染的,丙是受甲或乙感染的,假设他受甲和受乙感染的概率分别是![]() 和
和![]() .丁是受甲、乙或丙感染的,假设他受甲、乙和丙感染的概率分别是
.丁是受甲、乙或丙感染的,假设他受甲、乙和丙感染的概率分别是![]() 、
、![]() 和
和![]() .在这种假设之下,乙、丙、丁中直接受甲感染的人数为
.在这种假设之下,乙、丙、丁中直接受甲感染的人数为![]() .
.
(1)求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)该市在发现在本地出现新冠病毒感染者后,迅速采取应急措施,其中一项措施是各区必须每天及时,上报新增疑似病例人数.![]() 区上报的连续
区上报的连续![]() 天新增疑似病例数据是“总体均值为
天新增疑似病例数据是“总体均值为![]() ,中位数
,中位数![]() ”,
”,![]() 区上报的连续
区上报的连续![]() 天新增疑似病例数据是“总体均值为
天新增疑似病例数据是“总体均值为![]() ,总体方差为
,总体方差为![]() ”.设
”.设![]() 区和
区和![]() 区连续
区连续![]() 天上报新增疑似病例人数分别为
天上报新增疑似病例人数分别为![]() 和
和![]() ,
,![]() 和
和![]() 分别表示
分别表示![]() 区和
区和![]() 区第
区第![]() 天上报新增疑似病例人数(
天上报新增疑似病例人数(![]() 和
和![]() 均为非负).记
均为非负).记![]() ,
,![]() .
.
①试比较![]() 和
和![]() 的大小;
的大小;
②求![]() 和
和![]() 中较小的那个字母所对应的
中较小的那个字母所对应的![]() 个数有多少组?
个数有多少组?
【答案】(1)详见解析(2)①![]() ②
②![]() 组
组
【解析】
(1)记事件![]() “丙受甲感染”,事件
“丙受甲感染”,事件![]() “丁受甲感染”,则
“丁受甲感染”,则![]() ,
,![]() ,
,![]() 的取值为
的取值为![]() ,
,![]()
![]()
![]() ,再列出
,再列出![]() 的分布列并求期望.
的分布列并求期望.
(2)(i)对于![]() 区,根据“总体均值为
区,根据“总体均值为![]() ,总体方差为
,总体方差为![]() ”,有
”,有![]() ,再根据
,再根据![]() 是非负整数,得到
是非负整数,得到![]() ,从而确定
,从而确定![]() ,同理对于
,同理对于![]() 区,根据“总体均值为
区,根据“总体均值为![]() ,中位数
,中位数![]() ”,确定
”,确定![]() .(ii)当
.(ii)当![]() 时,只有两种组合,一是一个是
时,只有两种组合,一是一个是![]() ,五个是
,五个是![]() 或
或![]() ,一个是
,一个是![]() ;二是一个是
;二是一个是![]() ,一个是
,一个是![]() 或
或![]() ,一个是
,一个是![]() 或
或![]() ,其余是
,其余是![]() ,分别求得组数再求和.
,分别求得组数再求和.
(1)记事件![]() “丙受甲感染”,事件
“丙受甲感染”,事件![]() “丁受甲感染”,则
“丁受甲感染”,则![]() ,
,![]()
![]() 的取值为
的取值为![]()
![]()
![]()
![]()
所以![]() 的分布列为
的分布列为
| 1 | 2 | 3 |
| 0.32 | 0.56 | 0.12 |
![]()
(2)(i)对于![]() 区,由
区,由![]() 知,
知,
![]() ,因为
,因为![]() 是非负整数,
是非负整数,
所以![]() ,即
,即![]() ,所以
,所以![]()
当![]() 中有一个取
中有一个取![]() ,有一个取
,有一个取![]() ,其余取
,其余取![]() 时,
时,![]()
对于![]() 区,当
区,当![]() ,
,![]() ,
,![]() 时,满足“总体均值为
时,满足“总体均值为![]() ,中位数
,中位数![]() ”,此时,
”,此时,![]()
所以![]()
(ii)当![]() 时,
时,![]() 只有两种情况:
只有两种情况:
①有一个是![]() ,有五个是
,有五个是![]() 或
或![]() ,有一个是
,有一个是![]() ;
;
②有一个是![]() ,有一个是
,有一个是![]() 或
或![]() ,有一个是
,有一个是![]() 或
或![]() ,其余是
,其余是![]() .
.
对于①,共有![]() 组
组
对于②,共有![]() 组
组
故共有![]() 组
组


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】2020年春节期间,全国人民都在抗击“新型冠状病毒肺炎”的斗争中.当时武汉多家医院的医用防护物资库存不足,某医院甚至面临断货危机,南昌某生产商现有一批库存的医用防护物资,得知消息后,立即决定无偿捐赠这批医用防护物资,需要用A、B两辆汽车把物资从南昌紧急运至武汉.已知从南昌到武汉有两条合适路线选择,且选择两条路线所用的时间互不影响.据调查统计2000辆汽车,通过这两条路线从南昌到武汉所用时间的频数分布表如下:
所用的时间(单位:小时) |
|
|
|
|
路线1的频数 | 200 | 400 | 200 | 200 |
路线2的频数 | 100 | 400 | 400 | 100 |
假设汽车A只能在约定交货时间的前5小时出发,汽车B只能在约定交货时间的前6小时出发(将频率视为概率).为最大可能在约定时间送达这批物资,来确定这两车的路线.
(1)汽车A和汽车B应如何选择各自的路线.
(2)若路线1、路线2的“一次性费用”分别为3.2万元、1.6万元,且每车医用物资生产成本为40万元(其他费用忽略不计),以上费用均由生产商承担,作为援助金额的一部分.根据这两辆车到达时间分别计分,具体规则如下(已知两辆车到达时间相互独立,互不影响):
到达时间与约定时间的差x(单位:小时) |
|
|
|
该车得分 | 0 | 1 | 2 |
生产商准备根据运输车得分情况给出现金排款,两车得分和为0,捐款40万元,两车得分和每增加1分,捐款增加20万元,若汽车A、B用(1)中所选的路线运输物资,记该生产商在此次援助活动中援助总额为Y(万元),求随机变量Y的期望值,(援助总额![]() 一次性费用
一次性费用![]() 生产成本
生产成本![]() 现金捐款总额)
现金捐款总额)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的四个顶点围成的菱形的面积为
的四个顶点围成的菱形的面积为![]() ,椭圆的一个焦点为
,椭圆的一个焦点为![]() .
.
(1)求椭圆的方程;
(2)若![]() ,
,![]() 为椭圆上的两个动点,直线
为椭圆上的两个动点,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,当
,当![]() 时,
时,![]() 的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和圆
和圆![]() ,倾斜角为45°的直线
,倾斜角为45°的直线![]() 过抛物线
过抛物线![]() 的焦点,且
的焦点,且![]() 与圆
与圆![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)动点![]() 在抛物线
在抛物线![]() 的准线上,动点
的准线上,动点![]() 在
在![]() 上,若
上,若![]() 在
在![]() 点处的切线
点处的切线![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() .求证点
.求证点![]() 在定直线上,并求该定直线的方程.
在定直线上,并求该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 周长为8.
周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() ,使以
,使以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,若存在求出直线
,若存在求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解学生对《3.12植树节》活动节日的相关内容,学校进行了一次10道题的问卷调查,从该校学生中随机抽取50人,统计了每人答对的题数,将统计结果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,得到如下频率分布直方图.
五组,得到如下频率分布直方图.
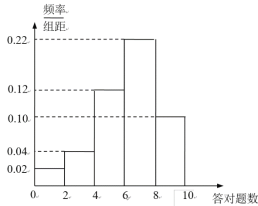
(1)若答对一题得10分,答错和未答不得分,估计这50名学生成绩的平均分;
(2)若从答对题数在![]() 内的学生中随机抽取2人,求恰有1人答对题数在
内的学生中随机抽取2人,求恰有1人答对题数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)当a=-1时,
①求曲线y= f(x)在点(0,f(0))处的切线方程;
②求函数f(x)的最小值;
(II)求证:当![]() 时,曲线
时,曲线![]() 与
与![]() 有且只有一个交点.
有且只有一个交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自湖北爆发新型冠状病毒肺炎疫情以来,湖北某市医护人员和医疗、生活物资严重匮乏,全国各地纷纷驰援.某运输队接到从武汉送往该市物资的任务,该运输队有8辆载重为6t的A型卡车,6辆载重为10t的B型卡车,10名驾驶员,要求此运输队每天至少运送240t物资.已知每辆卡车每天往返的次数为A型卡车5次,B型卡车4次,每辆卡车每天往返的成本A型卡车1200元,B型卡车1800元,则每天派出运输队所花的成本最低为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com