
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 底面
底面![]() ,
,![]()
![]() .
.
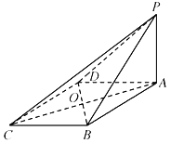
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由底面![]() 为菱形,得
为菱形,得![]() ,再由
,再由![]() 底面
底面![]() ,可得
,可得![]() ,结合线面垂直的判定可得
,结合线面垂直的判定可得![]() 平面
平面![]() ;
;
(2)以点![]() 为坐标原点,以
为坐标原点,以![]() 所在直线及过点
所在直线及过点![]() 且垂直于平面
且垂直于平面![]() 的直线分别为
的直线分别为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,分别求出平面
,分别求出平面![]() 与平面
与平面![]() 的一个法向量,由两法向量所成角的余弦值可得平面
的一个法向量,由两法向量所成角的余弦值可得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)证明:![]() 底面
底面![]() 为菱形,
为菱形,![]() ,
,
![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,![]()
又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ;
;
(2)解:![]() ,
,![]() ,
,![]() 为等边三角形,
为等边三角形,
![]() .
.
![]() 底面
底面![]() ,
,![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
在![]() 中,由
中,由![]() ,解得
,解得![]() .
.
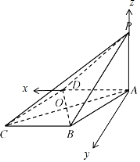
如图,以点![]() 为坐标原点,以
为坐标原点,以![]() 所在直线及过点
所在直线及过点![]() 且垂直于平面
且垂直于平面![]() 的直线分别为
的直线分别为![]() 轴
轴
建立空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 与平面
与平面![]() 的一个法向量分别为
的一个法向量分别为![]() ,
,![]() .
.
由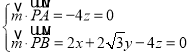 ,取
,取![]() ,得
,得![]() ;
;
由 ,取
,取![]() ,得
,得![]() .
.
 .
.
![]() 平面
平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当![]() 时,
时,![]() (
(![]() ).
).
(1)当![]() 时,求
时,求![]() 的表达式:
的表达式:
(2)求![]() 在区间
在区间![]() 的最大值
的最大值![]() 的表达式;
的表达式;
(3)当![]() 时,若关于x的方程
时,若关于x的方程![]() (a,
(a,![]() )恰有10个不同实数解,求a的取值范围.
)恰有10个不同实数解,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间之间坐标系![]() 中,四棱锥
中,四棱锥![]() 的底面
的底面![]() 在平面
在平面![]() 上,其中点
上,其中点![]() 与坐标原点
与坐标原点![]() 重合,点
重合,点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,顶点
,顶点![]() 在
在![]() 轴上,且
轴上,且![]() ,
,![]() .
.
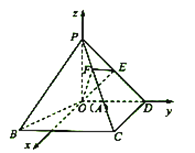
(1)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(2)设![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
(2)设![]() ,求证:存在唯一的
,求证:存在唯一的![]() ,使得函数
,使得函数![]() 的图象在点
的图象在点![]() 处的切线l与函数
处的切线l与函数![]() 的图象也相切;
的图象也相切;
(3)求证:对任意给定的正数a,总存在正数x,使得不等式![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
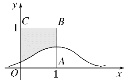
【题目】设X~N(1,σ2),其正态分布密度曲线如图所示,且P(X≥3)=0.0228,那么向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )
(附:随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
A. 6038 B. 6587 C. 7028 D. 7539
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的100人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 10 | 7 | 13 |
(1)若规定问卷得分不低于70分的市民称为“环保关注者”,请完成答题卡中的![]() 列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.视频率为概率.
①在我市所有“环保达人”中,随机抽取3人,求抽取的3人中,既有男“环保达人”又有女“环保达人”的概率;
②为了鼓励市民关注环保,针对此次的调查制定了如下奖励方案:“环保达人”获得两次抽奖活动;其他参与的市民获得一次抽奖活动.每次抽奖获得红包的金额和对应的概率.如下表:
红包金额(单位:元) | 10 | 20 |
概率 |
|
|
现某市民要参加此次问卷调查,记![]() (单位:元)为该市民参加间卷调查获得的红包金额,求
(单位:元)为该市民参加间卷调查获得的红包金额,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com