
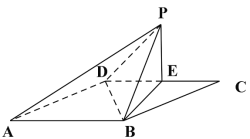
【题目】如图1,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 为
为![]() 的中点,以
的中点,以![]() 为折痕将
为折痕将![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如图2.
,如图2.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由题意可证得![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() 可证;
可证;
(2)解法一:利用等体积法由![]() 可求出点
可求出点![]() 到平面
到平面![]() 的距离;解法二:由条件知点
的距离;解法二:由条件知点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,过点
的距离,过点![]() 作
作![]() 的垂线,垂足
的垂线,垂足![]() ,证明
,证明![]() 平面
平面![]() ,计算出
,计算出![]() 即可.
即可.
解法一:(1)依题意知,因为![]() ,所以
,所以![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() .
.
由已知,![]() 是等边三角形,且
是等边三角形,且![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
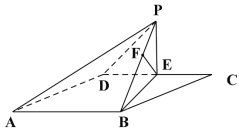
(2)在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() .
.
由(1)知,![]() 平面
平面![]() ,且
,且![]() ,
,
所以三棱锥![]() 的体积
的体积![]() .
.
在![]() 中,
中,![]() ,
,![]() ,得
,得![]() ,
,
由(1)知,![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() ,
,
设点![]() 到平面
到平面![]() 的距离
的距离![]() ,
,
则三棱锥![]() 的体积
的体积![]() ,得
,得![]() .
.
解法二:(1)同解法一;
(2)因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
过点![]() 作
作![]() 的垂线,垂足
的垂线,垂足![]() ,即
,即![]() .
.
由(1)知,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
由(1)知,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() .
.
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】在中国,不仅是购物,而且从共享单车到医院挂号再到公共缴费,日常生活中几乎全部领域都支持手机支付.出门不带现金的人数正在迅速增加。中国人民大学和法国调查公司益普索合作,调查了腾讯服务的6000名用户,从中随机抽取了60名,统计他们出门随身携带现金(单位:元)如茎叶图如示,规定:随身携带的现金在100元以下(不含100元)的为“手机支付族”,其他为“非手机支付族”.

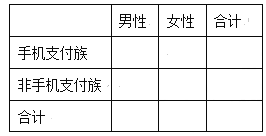
(1)根据上述样本数据,将![]() 列联表补充完整,并判断有多大的把握认为“手机支付族”与“性别”有关?
列联表补充完整,并判断有多大的把握认为“手机支付族”与“性别”有关?
(2)用样本估计总体,若从腾讯服务的用户中随机抽取3位女性用户,这3位用户中“手机支付族”的人数为![]() ,求随机变量
,求随机变量![]() 的期望和方差;
的期望和方差;
(3)某商场为了推广手机支付,特推出两种优惠方案,方案一:手机支付消费每满1000元可直减100元;方案二:手机支付消费每满1000元可抽奖2次,每次中奖的概率同为![]() ,且每次抽奖互不影响,中奖一次打9折,中奖两次打8.5折.如果你打算用手机支付购买某样价值1200元的商品,请从实际付款金额的数学期望的角度分析,选择哪种优惠方案更划算?
,且每次抽奖互不影响,中奖一次打9折,中奖两次打8.5折.如果你打算用手机支付购买某样价值1200元的商品,请从实际付款金额的数学期望的角度分析,选择哪种优惠方案更划算?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
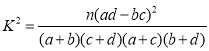
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地举行水上运动会,如图,岸边有![]() 两点,
两点,![]() ,小船从
,小船从![]() 点以
点以![]() 千米/小时的速度沿
千米/小时的速度沿![]() 方向匀速直线行驶,同一时刻运动员出发,经过
方向匀速直线行驶,同一时刻运动员出发,经过![]() 小时与小船相遇.(水流速度忽略不计)
小时与小船相遇.(水流速度忽略不计)
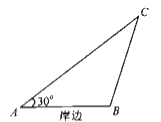
(1)若![]() ,
,![]() ,运动员从
,运动员从![]() 处出发游泳匀速直线追赶,为保证在1小时内(含1小时)能与小船相遇,试求运动员游泳速度的最小值;
处出发游泳匀速直线追赶,为保证在1小时内(含1小时)能与小船相遇,试求运动员游泳速度的最小值;
(2)若运动员先从![]() 处沿射线
处沿射线![]() 方向在岸边跑步匀速行进
方向在岸边跑步匀速行进![]() 小时后,再游泳匀速直线追赶小船.已知运动员在岸边跑步的速度为4千米小时,在水中游泳的速度为2千米小时,试求小船在能与运动员相遇的条件下
小时后,再游泳匀速直线追赶小船.已知运动员在岸边跑步的速度为4千米小时,在水中游泳的速度为2千米小时,试求小船在能与运动员相遇的条件下![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在非零常数
,如果存在非零常数![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为
的“似周期”为![]() ,那么它是周期为2的周期函数;
,那么它是周期为2的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③如果函数![]() 是“似周期函数”,那么“
是“似周期函数”,那么“![]() 或
或![]() ”.
”.
以上正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的面积的最大值为
的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,线段
,线段![]() 的中垂线为
的中垂线为![]() .若直线
.若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,点
,点![]() 分别为椭圆
分别为椭圆![]() 与坐标轴的交点,且
与坐标轴的交点,且![]() .过
.过![]() 轴上定点
轴上定点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为线段
为线段![]() 的中点.
的中点.
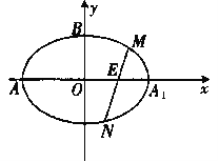
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地方政府召开全面展开新旧动能转换重大工程动员大会,动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前、后生产的大量产品中各抽取了200件作为样本,检测一项质量指标值.若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.如图所示的是设备改造前样本的频率分布直方图.
内的产品视为合格品,否则为不合格品.如图所示的是设备改造前样本的频率分布直方图.
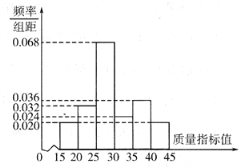
(1)若设备改造后样本的该项质量指标值服从正态分布![]() ,求改造后样本中不合格品的件数;
,求改造后样本中不合格品的件数;
(2)完成下面2×2列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量标值与设备改造有关.
0 | 设备改造前 | 设备改造后 | 合计 |
合格品件数 | |||
不合格品件数 | |||
合计 |
附参考公式和数据:
若![]() ,则
,则![]() ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
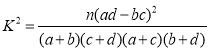
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com