
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,点
,点![]() 分别为椭圆
分别为椭圆![]() 与坐标轴的交点,且
与坐标轴的交点,且![]() .过
.过![]() 轴上定点
轴上定点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为线段
为线段![]() 的中点.
的中点.
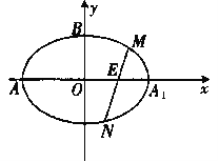
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题设知椭圆的离心率和![]() 的关系,结合
的关系,结合![]() ,求得
,求得![]() 的值,即可得到椭圆的标准方程;
的值,即可得到椭圆的标准方程;
(2)分直线MN的斜率为0和不为0两种情况讨论,设直线MN的方程与椭圆的方程联立,结合根与系数的关系,求得点Q的坐标,得出点Q到AB的距离,求得面积的表达式,利用基本不等式,即可求解.
(1)由题意,椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,
,
其中![]() ,
,![]() ,
,
由![]() ,得
,得![]() .
.
又由![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)直线![]() 的方程为
的方程为![]() ,
,
①当直线![]() 的斜率
的斜率![]() 时,直线过点
时,直线过点![]() 交椭圆于左右顶点,则中点为坐标原点
交椭圆于左右顶点,则中点为坐标原点![]() ,此时
,此时![]() ,
,
②当直线![]() 的斜率
的斜率![]() 时,设直线的方程为
时,设直线的方程为![]() ,
,
联立方程组 ,得
,得![]() ,∴点
,∴点![]() 为
为![]() ,
,
∴点![]() 到直线
到直线![]() 的距离
的距离![]() 为
为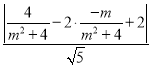 ,
,
∵点![]() 在直线
在直线![]() 的下方,即
的下方,即![]() ,
,
∴ ,
,
∴ ,
,
设![]() ,令
,令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时, ,
,
当且仅当![]() ,即
,即![]() 时等号成立,此时
时等号成立,此时 ,
,
当![]() 时,
时,![]() ,此时
,此时![]() ,
,
综上所述,![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知实数a满足1<a≤2,设函数f (x)=![]() x3-
x3-![]() x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于等于10.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
① 函数![]() 的最小正周期是
的最小正周期是![]() ;
;
② 函数![]() 在区间
在区间![]() 上是减函数;
上是减函数;
③ 函数![]() 的图像关于点
的图像关于点![]() 对称;
对称;
④ 函数![]() 的图像可由函数
的图像可由函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再向下平移1个单位得到.其中正确结论的个数是( )
个单位,再向下平移1个单位得到.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() 表示的曲线为
表示的曲线为![]() 的图象,对于函数
的图象,对于函数![]() 有如下结论:①
有如下结论:①![]() 在
在![]() 上单调递减;②函数
上单调递减;②函数![]() 至少存在一个零点;③
至少存在一个零点;③![]() 的最大值为
的最大值为![]() ;④若函数
;④若函数![]() 和
和![]() 图象关于原点对称,则
图象关于原点对称,则![]() 由方程
由方程![]() 所确定;则正确命题序号为( )
所确定;则正确命题序号为( )
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为矩形,AB=![]() ,BC=1,E,F分别是AB,PC的中点,DE⊥PA.
,BC=1,E,F分别是AB,PC的中点,DE⊥PA.
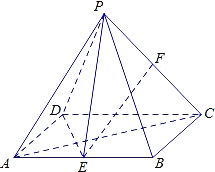
(1)求证:EF∥平面PAD;
(2)求证:平面PAC⊥平面PDE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com